
题目列表(包括答案和解析)
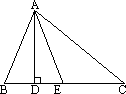
如图所示,△ABC中,∠B>∠C,AE平分∠BAC,若AD⊥BC于D,则∠DAE=![]() (∠B-∠C)
(∠B-∠C)
理由是∵AE平分∠BAC,∴∠BAE=∠CAE=![]() ∠BAC
∠BAC
又AD⊥BC于D,∴∠AED+∠DAE=![]()
又∠AED=∠C+∠EAC=∠C+![]() ∠BAC
∠BAC
∠DAE=![]() -∠C-
-∠C-![]() ∠BAC
∠BAC
=![]() -
-![]() (∠C+∠BAC)-
(∠C+∠BAC)-![]() ∠C
∠C
=![]() -
-![]() (
(![]() -∠B)-
-∠B)-![]() ∠C=
∠C=![]() (∠B-∠C)
(∠B-∠C)
如果点
P在AE上或AE的延长线上时,且PF⊥BC于F,那么∠FPE与∠B和∠C之间有什么关系?请选取图a、b所示中的两种图形中的任意一种加以说明.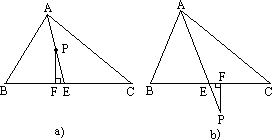
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com