练习册

  • 练习册
  • 试题
    17．如果将点(-b.-a)称为点(a.b)的“反称点 .那么点(a.b)也是点(-b.-a)的“反称点 .此时称点(a.b)和点(-b.-a)互为“反称点 ．容易发现.互为“反称点 的两个点有时是重合的.例如(0.0)的“反称点 还是(0.0)．请再写出一个这样的点: ▲ ． 【查看更多】

     

    题目列表(包括答案和解析)

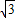    如图，在直角坐标系中，点A的坐标为（-1，），连接OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．
    （1）求点B的坐标；
    （2）求经过A、O、B三点的抛物线的解析式；
    （3）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．
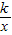    （4）若反比例函数y=（x＞0）的图象有一动点Q，点Q与抛物线上的点A关于点M（1，t）成中心对称，当以线段AB为一直角边的△QAB为直角三角形时，请直接写出相应的反比例函数的解析式．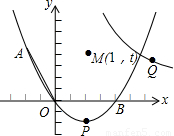

    查看答案和解析>>

    如果将点（-b，-a）称为点（a，b）的“反称点”，那么点（a，b）也是点（-b，-a）的“反称点”，此时，称点（a，b）和点（-b，-a）是互为“反称点”．容易发现，互为“反称点”的两点有时是重合的，例如（0，0）的“反称点”还是（0，0）．请再写出一个这样的点：

     

    查看答案和解析>>

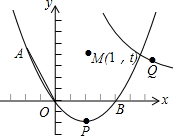    如图，在直角坐标系中，点A的坐标为（-1，
    		3
    ），连接OA，将线段OA绕原点O顺时针旋转120°，得到线段OB．
    （1）求点B的坐标；
    （2）求经过A、O、B三点的抛物线的解析式；
    （3）如果点P是（2）中的抛物线上的动点，且在x轴的下方，那么△PAB是否有最大面积？若有，求出此时P点的坐标及△PAB的最大面积；若没有，请说明理由．
    （4）若反比例函数y=
    k
    x
    （x＞0）的图象有一动点Q，点Q与抛物线上的点A关于点M（1，t）成中心对称，当以线段AB为一直角边的△QAB为直角三角形时，请直接写出相应的反比例函数的解析式．

    查看答案和解析>>

    全等三角形又叫做合同三角形，平面内的合同三角形分为真正合同三角形和镜面合同三角形，假设△ABC和△A1B1C1是全等（合同）三角形，且点A与点A1对应，点B与点B1对应，点C与点C1对应，当沿周界A→B→C→A及A1→B1→C1→A1环绕时，若运动方向相同，则称它们是真正合同三角形（如图1）；若运动方向相反，则称它们是镜面合同三角形（如图2）。

          图1                            图2
    两个真正合同三角形，都可以在平面内通过平移或旋转使它们重合；而两个镜面合同三角形要重合，则必须将其中的一个翻转180°，下图中的各组合同三角形中，有没有镜面合同三角形？如果有，是哪几个，并说明理由。

    查看答案和解析>>

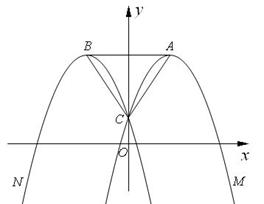
    已知抛物线M：y = -x2+2mx+n（m，n为常数，且m> 0，n>0）的顶点为A，与y轴交于点C；抛物线N与抛物线M关于y轴对称，其顶点为B，连结AC，BC，AB．

    问抛物线M上是否存在点P，使得四边形ABCP为菱形？如果存在，请求出m的值；如果不存在，请说明理由．

    说明：⑴如果你反复探索,没有解决问题, 请写出探索过程(要求至少写3步)；

    ⑵在你完成⑴之后,可以从①、②中选取一个条件，完成解答（选取①得7分；选取②得10分）．

    ①；②．

    附加题: 若将26题中“抛物线M：y= -x2+2mx+n（m，n为常数，且m> 0，n>0） ”改为“抛物线M：y= ax2+2mx+n（m，n为常数，且m≠ 0,a≠0, n>0） ”，其他条件不变, 探究 26题中问题．

    查看答案和解析>>


    同步练习册答案