
题目列表(包括答案和解析)
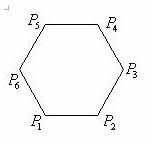
如图, 已知正六边形![]() ,下列向量的数量积中最大的是
,下列向量的数量积中最大的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
如图, 已知正六边形![]() ,下列向量的数量积中最大的是
,下列向量的数量积中最大的是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
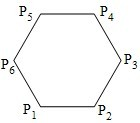 如图,已知正六边形P1P2P3P4P5P6,下列向量的数量积中最大的是( )
如图,已知正六边形P1P2P3P4P5P6,下列向量的数量积中最大的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
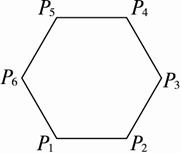
图2-4-1
A.![]() ,
,![]() B.
B.![]() ,
,![]() C.
C.![]() ,
,![]() D.
D.![]() ,
,![]()
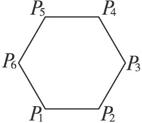
A.![]() B.
B.![]()
C.![]() D.
D.![]()
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至2页。第Ⅱ卷3到10页。考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其它答案标号。不能答在试题卷上。
3.本卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
参考公式:
如果事件A、B互斥,那么 球是表面积公式
如果事件A、B相互独立,那么 其中R表示球的半径
球的体积公式
如果事件A在一次试验中发生的概率是P,那么
n次独立重复试验中恰好发生k次的概率 其中R表示球的半径
一.选择题:本大题共12小题,每小题5分,共60分;
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
D
B
A
C
(1)已知集合,集合,则集合
(A) (B)
(C) (D)
(2)函数的反函数是
(A) (B)
(C) (D)
(3)曲线在点处的切线方程是
(A) (B)
(C) (D)
(4)如图,已知正六边形,下列向量的数量积中最大的是
(A) (B)
(C) (D)
(5)甲校有名学生,乙校有名学生,丙校有名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个容量为人的样本,应在这三校分别抽取学生
(A)人,人,人 (B)人,人,人
(C)人,人,人 (D)人,人,人
(6)下列函数中,图象的一部分如右图所示的是
(A) (B)
(C) (D)
(7) 已知二面角的大小为,为异面直线,且,则所成的角为
(A) (B) (C) (D)
(8) 已知两定点,如果动点满足,则点的轨迹所包围的图形的面积等于
(A) (B) (C) (D)
(9) 如图,正四棱锥底面的四个顶点在球的同一
个大圆上,点在球面上,如果,则球的表面积是
(A) (B) (C) (D)
(10) 直线与抛物线交于两点,过两点向抛物线的准线
作垂线,垂足分别为,则梯形的面积为
(A) (B) (C) (D)
(11)设分别是的三个内角所对的边,则是的
(A)充分条件 (B)充分而不必要条件
(C)必要而充分条件 (D)既不充分又不必要条件
(12)从到这个数字中任取个数字组成一个没有重复数字的三位数,这个数不能被整除的概率为
(A) (B) (C) (D)
第Ⅱ卷
二.填空题:本大题共4小题,每小题4分,共16分;把答案填在题中的横线上。
(13)展开式中的系数为________________(用数字作答)
(14)设满足约束条件:,则的最小值为________________;
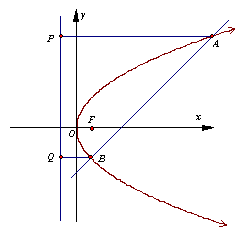
(15)如图,把椭圆的长轴分成等份,过每个分点作轴的垂线交椭圆的上半部分于七个点,是椭圆的一个焦点,则
________________;
(16)是空间两条不同直线,是两个不同平面,下面有四个命题:
① ②
③ ④
其中真命题的编号是_______①,②_________;(写出所有真命题的编号)
三.解答题:本大题共6小题,共74分;解答应写出文字说明,证明过程或演算步骤。
(17)(本大题满分12分)
数列的前项和记为
(Ⅰ)求的通项公式;
(Ⅱ)等差数列的各项为正,其前项和为,且,又成等比数列,求
本小题主要考察等差数列、等比数列的基础知识,以及推理能力与运算能力。满分12分。
解:(Ⅰ)由可得,两式相减得
又 ∴
故是首项为,公比为得等比数列
∴
(Ⅱ)设的公比为
由得,可得,可得
故可设
又
由题意可得
解得
∵等差数列的各项为正,∴
∴
∴
(18)(本大题满分12分)
已知是三角形三内角,向量,且
(Ⅰ)求角;
(Ⅱ)若,求
本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公式,考察应用、分析和计算能力。满分12分。
解:(Ⅰ)∵ ∴
即
∵
∴
∴
(Ⅱ)由题知,整理得
∴ ∴
∴或
而使,舍去
∴
(19)(本大题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为;在实验考核中合格的概率分别为,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解决实际问题的能力。满分12分。
解:记“甲理论考核合格”为事件,“乙理论考核合格”为事件,“丙理论考核合格”为事件, 记为的对立事件,;记“甲实验考核合格”为事件,“乙实验考核合格”为事件,“丙实验考核合格”为事件,
(Ⅰ)记“理论考核中至少有两人合格”为事件,记为的对立事件
解法1:
解法2:
所以,理论考核中至少有两人合格的概率为
(Ⅱ)记“三人该课程考核都合格” 为事件
所以,这三人该课程考核都合格的概率为
(20)(本大题满分12分)
如图,在长方体中,分别是的
中点,分别是的中点,
(Ⅰ)求证:面;
(Ⅱ)求二面角的大小。
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。满分12分
解法一:
(Ⅰ)证明:取的中点,连结
∵分别为的中点
∵
∴面,面
∴面面
∴面
(Ⅱ)设为的中点
∵为的中点 ∴
∴面
作,交于,连结,则由三垂线定理得
从而为二面角的平面角。
在中,,从而
在中,
故:二面角的大小为
方法二:以为原点,所在直线分别为轴,轴,轴,建立直角坐标系,则
∵分别是的中点
∴
(Ⅰ)
取,显然面
,∴
又面
∴面
∴过作,交于,取的中点,则
设,则
又
由,及在直线上,可得:
解得
∴
∴ 即
∴与所夹的角等于二面角的大小
故:二面角的大小为
(21)(本大题满分12分)
已知函数,其中是的导函数
(Ⅰ)对满足的一切的值,都有,求实数的取值范围;
(Ⅱ)设,当实数在什么范围内变化时,函数的图象与直线只有一个公共点
本小题主要考察函数的单调性、导数的应用、解不等式等基础知识,以及推理能力、运输能力和综合应用数学知识的能力。满分12分。
解:(Ⅰ)由题意
令,
对,恒有,即
∴ 即
解得
故时,对满足的一切的值,都有
(Ⅱ)
①当时,的图象与直线只有一个公共点
②当时,列表:
极大
极小
∴
又∵的值域是,且在上单调递增
∴当时函数的图象与直线只有一个公共点。
当时,恒有
由题意得
即
解得
综上,的取值范围是
(22)(本大题满分14分)
已知两定点,满足条件的点的轨迹是曲线,直线与曲线交于两点
(Ⅰ)求的取值范围;
(Ⅱ)如果,且曲线上存在点,使,求的值和的面积
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力。满分14分。
解:(Ⅰ)由双曲线的定义可知,曲线是以为焦点的双曲线的左支,
且,易知
故曲线的方程为
设,由题意建立方程组
消去,得
又已知直线与双曲线左支交于两点,有
解得
∵
依题意得
整理后得
∴或
但 ∴
故直线的方程为
设,由已知,得
∴,
又,
∴点
将点的坐标代入曲线的方程,得得,
但当时,所得的点在双曲线的右支上,不合题意
∴,点的坐标为
到的距离为
∴的面积
录入:四川省内江市隆昌县黄家中学
程 亮
2006年普通高等学校招生全国统一考试
(四川卷)文科数学及参考答案
一.选择题:本大题共12小题,每小题5分,共60分;
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
D
B
A
C
(1)已知集合=,集合,则集合,选C.
(2)函数,解得(y∈R),所以原函数的反函数是,选A.
(3)曲线,导数,在点处的切线的斜率为,所以切线方程是,选D.
(4)如图,已知正六边形,设边长,则∠=.,,=,∠=,,=,=0,<0,∴ 数量积中最大的是,选A
(5)甲校有名学生,乙校有名学生,丙校有名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个容量为人的样本,应在这三校分别抽取学生人,人,人,选B.
(6)从图象看出,T=,所以函数的最小正周期为π,函数应为y=向左平移了个单位,即
=,所以选D.
(7) 已知二面角的大小为,为异面直线,且,则所成的角为两条直线所成的角,∴ θ=,选B.
(8) 已知两定点,如果动点满足,设P点的坐标为(x,y),
则,即,所以点的轨迹所包围的图形的面积等于4π,选C.
(9) 如图,正四棱锥底面的四个顶点在球的同一个大圆上,点在球面上,PO⊥底面ABCD,PO=R,,,所以,R=2,球的表面积是,选D.
(10) 直线与抛物线交于两点,过两点向抛物线的准线作垂线,垂足分别为,联立方程组得,消元得,解得,和,∴ |AP|=10,|BQ|=2,|PQ|=8,梯形的面积为48,选B.
(11)设分别是的三个内角所对的边,若,
则,则,
∴ ,,
又,∴ ,∴ ,,
若△ABC中,,由上可知,每一步都可以逆推回去,得到,
所以是的充要条件,选A.
(12)从到这个数字中任取个数字组成一个没有重复数字的三位数,这个数不能被整除。
所有的三位数有个,将10个数字分成三组,即被3除余1的有{1,4,7}、被3除余2的有{2,5,8},被3整除的有{3,6,9,0},若要求所得的三位数被3整除,则可以分类讨论:①三个数字均取第一组,或均取第二组,有个;② 若三个数字均取自第三组,则要考虑取出的数字中有无数字0,共有个;③ 若三组各取一个数字,第三组中不取0,有个,④若三组各取一个数字,第三组中取0,有个,这样能被3 整除的数共有228个,不能被整除的数有420个,所以概率为=,选C。
第Ⅱ卷
二.填空题:本大题共4小题,每小题4分,共16分;把答案填在题中的横线上。
(13)展开式中的项为,的系数为-960。
(14)设满足约束条件:,在直角坐标系中画出可行域△ABC,其中A(1,),B(1,8),C(4,2),所以的最小值为-6。
(15)如图,把椭圆的长轴分成等份,过每个分点作轴的垂线交椭圆的上半部分于七个点,是椭圆的一个焦点,则根据椭圆的对称性知,,同理其余两对的和也是,又,∴ =35.
(16)是空间两条不同直线,是两个不同平面,下面有四个命题:
①,为真命题;②,为ie假命题;
③为假命题; ④为真命题,
所以真命题的编号是①、④.
三.解答题:本大题共6小题,共74分;解答应写出文字说明,证明过程或演算步骤。
(17)(本大题满分12分)
数列的前项和记为
(Ⅰ)求的通项公式;
(Ⅱ)等差数列的各项为正,其前项和为,且,又成等比数列,求
本小题主要考察等差数列、等比数列的基础知识,以及推理能力与运算能力。满分12分。
解:(Ⅰ)由可得,两式相减得
又 ∴
故是首项为,公比为得等比数列
∴
(Ⅱ)设的公比为
由得,可得,可得
故可设
又
由题意可得
解得
∵等差数列的各项为正,∴
∴
∴
(18)(本大题满分12分)
已知是三角形三内角,向量,且
(Ⅰ)求角;
(Ⅱ)若,求
本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公式,考察应用、分析和计算能力。满分12分。
解:(Ⅰ)∵ ∴
即
∵
∴
∴
(Ⅱ)由题知,整理得
∴ ∴
∴或
而使,舍去
∴
(19)(本大题满分12分)
某课程考核分理论与实验两部分进行,每部分考核成绩只记“合格”与“不合格”,两部分考核都是“合格”则该课程考核“合格”,甲、乙、丙三人在理论考核中合格的概率分别为;在实验考核中合格的概率分别为,所有考核是否合格相互之间没有影响
(Ⅰ)求甲、乙、丙三人在理论考核中至少有两人合格的概率;
(Ⅱ)求这三人该课程考核都合格的概率。(结果保留三位小数)
本小题主要考察相互独立事件、互斥事件、对立事件等概率的计算方法,考察应用概率知识解决实际问题的能力。满分12分。
解:记“甲理论考核合格”为事件,“乙理论考核合格”为事件,“丙理论考核合格”为事件, 记为的对立事件,;记“甲实验考核合格”为事件,“乙实验考核合格”为事件,“丙实验考核合格”为事件,
(Ⅰ)记“理论考核中至少有两人合格”为事件,记为的对立事件
解法1:
解法2:
所以,理论考核中至少有两人合格的概率为
(Ⅱ)记“三人该课程考核都合格” 为事件
所以,这三人该课程考核都合格的概率为
(20)(本大题满分12分)
如图,在长方体中,分别是的
中点,分别是的中点,
(Ⅰ)求证:面;
(Ⅱ)求二面角的大小。
本小题主要考察长方体的概念、直线和平面、平面和平面的关系等基础知识,以及空间想象能力和推理能力。满分12分
解法一:
(Ⅰ)证明:取的中点,连结
∵分别为的中点
∵
∴面,面
∴面面
∴面
(Ⅱ)设为的中点
∵为的中点 ∴
∴面
作,交于,连结,则由三垂线定理得
从而为二面角的平面角。
在中,,从而
在中,
故:二面角的大小为
方法二:以为原点,所在直线分别为轴,轴,轴,建立直角坐标系,则
∵分别是的中点
∴
(Ⅰ)
取,显然面
,∴
又面
∴面
∴过作,交于,取的中点,则
设,则
又
由,及在直线上,可得:
解得
∴
∴ 即
∴与所夹的角等于二面角的大小
故:二面角的大小为
(21)(本大题满分12分)
已知函数,其中是的导函数
(Ⅰ)对满足的一切的值,都有,求实数的取值范围;
(Ⅱ)设,当实数在什么范围内变化时,函数的图象与直线只有一个公共点
本小题主要考察函数的单调性、导数的应用、解不等式等基础知识,以及推理能力、运输能力和综合应用数学知识的能力。满分12分。
解:(Ⅰ)由题意
令,
对,恒有,即
∴ 即
解得
故时,对满足的一切的值,都有
(Ⅱ)
①当时,的图象与直线只有一个公共点
②当时,列表:
极大
极小
∴
又∵的值域是,且在上单调递增
∴当时函数的图象与直线只有一个公共点。
当时,恒有
由题意得
即
解得
综上,的取值范围是
(22)(本大题满分14分)
已知两定点,满足条件的点的轨迹是曲线,直线与曲线交于两点
(Ⅰ)求的取值范围;
(Ⅱ)如果,且曲线上存在点,使,求的值和的面积
本小题主要考察双曲线的定义和性质、直线与双曲线的关系、点到直线的距离等知识及解析几何的基本思想、方法和综合解决问题的能力。满分14分。
解:(Ⅰ)由双曲线的定义可知,曲线是以为焦点的双曲线的左支,
且,易知
故曲线的方程为
设,由题意建立方程组
消去,得
又已知直线与双曲线左支交于两点,有
解得
∵
依题意得
整理后得
∴或
但 ∴
故直线的方程为
设,由已知,得
∴,
又,
∴点
将点的坐标代入曲线的方程,得得,
但当时,所得的点在双曲线的右支上,不合题意
∴,点的坐标为
到的距离为
∴的面积
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com