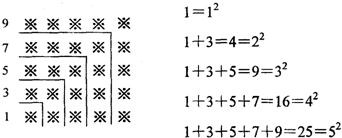解答题
①当m取何值时,关于x的方程:3x-2=4与5x-1=-m的解相等?
②一堆小麦用8个编织袋来装,以每袋55千克为标准,超过的记作为正数,不足的记作为负数,现记录如下:(单位:千克)
+2,-3,+2,+1,-2,-1,0,-2
(1)这堆小麦共重多少千克?
(2)若每千克小麦的售价为1.2元,则这堆小麦可卖多少钱?
③探索规律:观察下面由“※”组成的图案和算式,解答问题:
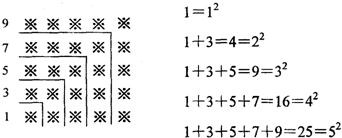
(1)请猜想1+3+5+7+9+…+19=
;
(2)请猜想1+3+5+7+9+…+(2n-1)+(2n+1)=
;
(3)请用上述规律计算:103+105+107+…+2003+2005.
④在左边的日历中,用一个正方形任意圈出二行二列四个数,
如

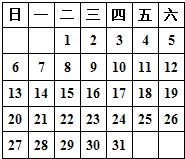
若在第二行第二列的那个数表示为a,其余各数分别为b,c,d.
如
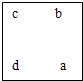
(1)分别用含a的代数式表示b,c,d这三个数.
(2)求这四个数的和(用含a的代数式表示,要求合并同类项化简)
(3)这四个数的和会等于51吗?如果会,请算出此时a的值,如果不会,说明理由.(要求列方程解答)

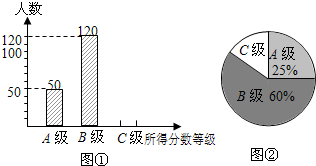 <8;C级:0≤x<4,并将调查结果绘制成图①和图②的统计图(不完整).
<8;C级:0≤x<4,并将调查结果绘制成图①和图②的统计图(不完整).