
题目列表(包括答案和解析)
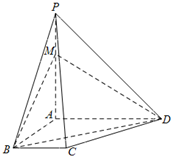 四棱锥P-ABCD中,PA⊥底面ABCD,其中底面ABCD为梯形,AD∥BC,AB⊥BC,且AP=AB=AD=2BC=6,M在棱PA上,满足AM=2MP.
四棱锥P-ABCD中,PA⊥底面ABCD,其中底面ABCD为梯形,AD∥BC,AB⊥BC,且AP=AB=AD=2BC=6,M在棱PA上,满足AM=2MP.
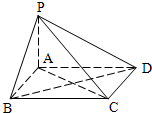 若四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD(如图),且PA=2
若四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD(如图),且PA=2| 3 |
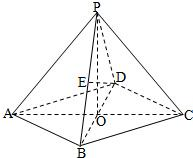 在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°.
在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成的角为60°.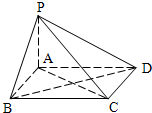 若四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD(如图),且
若四棱锥P-ABCD的底面是边长为2的正方形,PA⊥底面ABCD(如图),且 .
.一.填空题:
1.试题.files/image191.gif) ; 2.
; 2.试题.files/image193.gif) ;
3.
;
3.试题.files/image195.gif) 4.2; 5.4;
4.2; 5.4;
6.45; 7.试题.files/image197.gif) ; 8.8;
9.3; 10.
; 8.8;
9.3; 10.试题.files/image199.gif) .
.
二.选择题:11.B ; 12. C; 13. C.
三.解答题:
15.解:(Ⅰ)由已知可求得,正方形试题.files/image201.gif) 的面积
的面积试题.files/image203.gif) ,……………………………2分
,……………………………2分
所以,求棱锥试题.files/image205.gif) 的体积
的体积试题.files/image207.gif) ………………………………………4分
………………………………………4分
(Ⅱ)方法一(综合法)
设线段试题.files/image209.gif) 的中点为
的中点为试题.files/image211.gif) ,连接
,连接试题.files/image213.gif) ,
,
则试题.files/image215.gif) 为异面直线OC与
为异面直线OC与试题.files/image217.gif) 所成的角(或其补角) ………………………………..1分
所成的角(或其补角) ………………………………..1分
由已知,可得试题.files/image219.gif) ,
,
试题.files/image221.gif)
试题.files/image223.gif) 为直角三角形 ……………………………………………………………….2分
为直角三角形 ……………………………………………………………….2分
试题.files/image225.gif) , ……………………………………………………………….4分
, ……………………………………………………………….4分
试题.files/image227.gif) .
.
所以,异面直线OC与MD所成角的大小试题.files/image229.gif) .
…………………………..1分
.
…………………………..1分
方法二(向量法)
以AB,AD,AO所在直线为试题.files/image024.gif) 轴建立坐标系,
轴建立坐标系,
则试题.files/image232.gif) , ……………………………………………………2分
, ……………………………………………………2分
试题.files/image234.gif) ,
,试题.files/image236.gif) , ………………………………………………………………………………..2分
, ………………………………………………………………………………..2分
设异面直线OC与MD所成角为试题.files/image238.gif) ,
,
试题.files/image240.gif) .………………………………..
…………………………3分
.………………………………..
…………………………3分
试题.files/image242.gif) OC与MD所成角的大小为
OC与MD所成角的大小为试题.files/image244.gif) .…………………………………………………1分
.…………………………………………………1分
16.[解一]由已知,在试题.files/image246.gif) 中,
中,试题.files/image248.gif) ,
,试题.files/image250.gif) ,………………………….2分
,………………………….2分
由正弦定理,得试题.files/image252.gif)
试题.files/image254.gif) ……………………………6分
……………………………6分
因此,试题.files/image256.gif)
试题.files/image258.gif) …………………………………………5分
…………………………………………5分
试题.files/image260.gif) .……………………………………………………………………2分
.……………………………………………………………………2分
[解二] 延长试题.files/image089.gif) 交地平线与
交地平线与试题.files/image263.gif) ,…………………………………………………………………3分
,…………………………………………………………………3分
由已知,得试题.files/image265.gif) …………………………………………………4分
…………………………………………………4分
整理,得试题.files/image104.gif) ………………………………………………………………………8分
………………………………………………………………………8分
17.[解](Ⅰ)函数试题.files/image110.gif) 的定义域为
的定义域为试题.files/image269.gif) …………………………………………………………2分
…………………………………………………………2分
试题.files/image271.gif) ,
,
当试题.files/image108.gif) 时,因为
时,因为试题.files/image274.gif) ,所以
,所以试题.files/image276.gif) ,
,
试题.files/image278.gif) ,从而
,从而试题.files/image280.gif) ,……………………………………………………..4分
,……………………………………………………..4分
所以函数试题.files/image110.gif) 的值域为
的值域为试题.files/image283.gif) .………………………………………………………………..1分
.………………………………………………………………..1分
(Ⅱ)假设函数试题.files/image110.gif) 是奇函数,则,对于任意的
是奇函数,则,对于任意的试题.files/image285.gif) ,有
,有试题.files/image287.gif) 成立,
成立,
即试题.files/image289.gif)
试题.files/image291.gif) 当
当试题.files/image293.gif) 时,函数
时,函数试题.files/image110.gif) 是奇函数.…………………………………………………………….3分
是奇函数.…………………………………………………………….3分
当试题.files/image108.gif) ,且
,且试题.files/image295.gif) 时,函数
时,函数试题.files/image110.gif) 是非奇非偶函数.………………………………………….1分
是非奇非偶函数.………………………………………….1分
试题.files/image297.gif) 对于任意的
对于任意的试题.files/image299.gif) ,且
,且试题.files/image301.gif) ,
,
试题.files/image303.gif)
试题.files/image305.gif)
试题.files/image307.gif) ……………………………………………..4分
……………………………………………..4分
试题.files/image291.gif) 当
当试题.files/image108.gif) 时,函数
时,函数试题.files/image110.gif) 是递减函数.………………………………………………..1分
是递减函数.………………………………………………..1分
18.[解](Ⅰ)因为试题.files/image122.gif) ,且
,且试题.files/image089.gif) 边通过点
边通过点试题.files/image310.gif) ,所以
,所以试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image313.gif) .1分
.1分
设试题.files/image115.gif) 两点坐标分别为
两点坐标分别为试题.files/image316.gif) .
.
由试题.files/image318.gif) 得
得试题.files/image320.gif) .
.
所以试题.files/image322.gif) . ……………………………………………..4分
. ……………………………………………..4分
又因为试题.files/image089.gif) 边上的高
边上的高试题.files/image093.gif) 等于原点到直线
等于原点到直线试题.files/image326.gif) 的距离.
的距离.
所以试题.files/image328.gif) ,
,试题.files/image330.gif) . ……………………………………….3分
. ……………………………………….3分
(Ⅱ)设试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image333.gif) , ……………………………………………..1分
, ……………………………………………..1分
由试题.files/image335.gif) 得
得试题.files/image337.gif) . …………………………………..2分
. …………………………………..2分
因为试题.files/image115.gif) 在椭圆上,所以
在椭圆上,所以试题.files/image340.gif) . ………………….. …………..1分
. ………………….. …………..1分
设试题.files/image115.gif) 两点坐标分别为
两点坐标分别为试题.files/image316.gif) ,
,
则试题.files/image344.gif) ,
,试题.files/image346.gif) ,
,
所以试题.files/image348.gif) .……………………………………………..3分
.……………………………………………..3分
又因为试题.files/image350.gif) 的长等于点
的长等于点试题.files/image352.gif) 到直线
到直线试题.files/image326.gif) 的距离,即
的距离,即试题.files/image355.gif) .……………..2分
.……………..2分
所以试题.files/image357.gif) .…………………..2分
.…………………..2分
所以当试题.files/image359.gif) 时,
时,试题.files/image131.gif) 边最长,(这时
边最长,(这时试题.files/image362.gif) )
)
此时试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image365.gif) . ……………………………………………..1分
. ……………………………………………..1分
17.[解](Ⅰ)由题意,试题.files/image367.gif) ……………………………6分
……………………………6分
(Ⅱ)解法1:由试题.files/image172.gif) 且
且试题.files/image178.gif) 知
知
试题.files/image370.gif) ,
,试题.files/image372.gif) ,
,试题.files/image374.gif)
试题.files/image376.gif) ,
,试题.files/image378.gif) ,
,试题.files/image380.gif)
因此,可猜测试题.files/image382.gif) (
(试题.files/image174.gif) ) ………………………………………………………4分
) ………………………………………………………4分
将试题.files/image382.gif) ,
,试题.files/image385.gif) 代入原式左端得
代入原式左端得
左端试题.files/image387.gif)
试题.files/image389.gif)
试题.files/image391.gif)
即原式成立,故试题.files/image382.gif) 为数列的通项.……………………………………………………….3分
为数列的通项.……………………………………………………….3分
用数学归纳法证明得3分
解法2:由 试题.files/image178.gif) ,
,试题.files/image176.gif)
令试题.files/image395.gif) 得
得试题.files/image397.gif) ,且
,且试题.files/image399.gif)
即试题.files/image401.gif) ,……… ……………………………………………………………..4分
,……… ……………………………………………………………..4分
所以试题.files/image403.gif)
因此试题.files/image405.gif) ,
,试题.files/image407.gif) ,...,
,...,试题.files/image409.gif)
将各式相乘得试题.files/image382.gif) ………………………………………………………………………………3分
………………………………………………………………………………3分
(Ⅲ)设上表中每行的公比都为试题.files/image412.gif) ,且
,且试题.files/image414.gif) .因为
.因为试题.files/image416.gif) ,
,
所以表中第1行至第9行共含有数列试题.files/image166.gif) 的前63项,故
的前63项,故试题.files/image418.gif) 在表中第10行第三列,………2分
在表中第10行第三列,………2分
因此试题.files/image420.gif) .又
.又试题.files/image422.gif) ,所以
,所以试题.files/image424.gif) .…………………………………..3分
.…………………………………..3分
则试题.files/image426.gif) .
.试题.files/image187.gif) …………………………………………2分
…………………………………………2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com