
题目列表(包括答案和解析)
 将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知:
将数列{an} 中的所有项按第一排三项,以下每一行比上一行多一项的规则排成如数表:记表中的第一列数a1,a4,a8,…构成的数列为{bn},已知: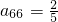 .请解答以下问题:
.请解答以下问题: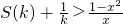 在
在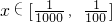 上有解,求正整数k的取值范围.
上有解,求正整数k的取值范围.a1
a2 a3
a4 a5 a6
a7 a8 a9 a10记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1=1,Sn为数列{bn}的前n项和,且满足![]() =1(n≥2).
=1(n≥2).
(Ⅰ)证明数列![]() 成等差数列,并求数列{bn}的通项公式;
成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数,当![]() 时,求上表中第k(k≥3)行所有项的和.
时,求上表中第k(k≥3)行所有项的和.
将正数数列![]() 中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数
中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数![]() 构成数列为
构成数列为![]() ,各行的最后一个数
,各行的最后一个数![]() 构成数列为
构成数列为![]() ,第
,第![]() 行所有数的和为
行所有数的和为![]()
![]() 。已知数列
。已知数列![]() 是公差为
是公差为![]() 的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数
的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式。
的通项公式。
(2)求数列![]() 的前
的前![]() 项和
项和![]() 的表达式.
的表达式.
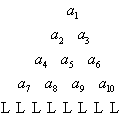 将正数数列
将正数数列![]() 中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数
中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数![]() 构成数列为
构成数列为![]() ,各行的最后一个数
,各行的最后一个数![]() 构成数列为
构成数列为![]() ,第
,第![]() 行所有数的和为
行所有数的和为![]()
![]() 。已知数列
。已知数列![]() 是公差为
是公差为![]() 的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数
的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式。
的通项公式。
(2)求数列![]() 的前
的前![]() 项和
项和![]() 的表达式.
的表达式.
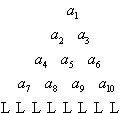 将正数数列
将正数数列![]() 中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数
中的所有项按每一行比上一行多一项的规则排成数表,如图所示。记表中各行的第一个数![]() 构成数列为
构成数列为![]() ,各行的最后一个数
,各行的最后一个数![]() 构成数列为
构成数列为![]() ,第
,第![]() 行所有数的和为
行所有数的和为![]()
![]() 。已知数列
。已知数列![]() 是公差为
是公差为![]() 的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数
的等差数列,从第二行起,每一行中的数按照从左到右的顺序每一个数与它前面一个数的比是常数![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式。
的通项公式。
(2)(理科)记![]()
![]() ,
,
求证:![]() 。
。
一.填空题:
1.试题.files/image191.gif) ; 2.
; 2.试题.files/image193.gif) ;
3.
;
3.试题.files/image195.gif) 4.2; 5.4;
4.2; 5.4;
6.45; 7.试题.files/image197.gif) ; 8.8;
9.3; 10.
; 8.8;
9.3; 10.试题.files/image199.gif) .
.
二.选择题:11.B ; 12. C; 13. C.
三.解答题:
15.解:(Ⅰ)由已知可求得,正方形试题.files/image201.gif) 的面积
的面积试题.files/image203.gif) ,……………………………2分
,……………………………2分
所以,求棱锥试题.files/image205.gif) 的体积
的体积试题.files/image207.gif) ………………………………………4分
………………………………………4分
(Ⅱ)方法一(综合法)
设线段试题.files/image209.gif) 的中点为
的中点为试题.files/image211.gif) ,连接
,连接试题.files/image213.gif) ,
,
则试题.files/image215.gif) 为异面直线OC与
为异面直线OC与试题.files/image217.gif) 所成的角(或其补角) ………………………………..1分
所成的角(或其补角) ………………………………..1分
由已知,可得试题.files/image219.gif) ,
,
试题.files/image221.gif)
试题.files/image223.gif) 为直角三角形 ……………………………………………………………….2分
为直角三角形 ……………………………………………………………….2分
试题.files/image225.gif) , ……………………………………………………………….4分
, ……………………………………………………………….4分
试题.files/image227.gif) .
.
所以,异面直线OC与MD所成角的大小试题.files/image229.gif) .
…………………………..1分
.
…………………………..1分
方法二(向量法)
以AB,AD,AO所在直线为试题.files/image024.gif) 轴建立坐标系,
轴建立坐标系,
则试题.files/image232.gif) , ……………………………………………………2分
, ……………………………………………………2分
试题.files/image234.gif) ,
,试题.files/image236.gif) , ………………………………………………………………………………..2分
, ………………………………………………………………………………..2分
设异面直线OC与MD所成角为试题.files/image238.gif) ,
,
试题.files/image240.gif) .………………………………..
…………………………3分
.………………………………..
…………………………3分
试题.files/image242.gif) OC与MD所成角的大小为
OC与MD所成角的大小为试题.files/image244.gif) .…………………………………………………1分
.…………………………………………………1分
16.[解一]由已知,在试题.files/image246.gif) 中,
中,试题.files/image248.gif) ,
,试题.files/image250.gif) ,………………………….2分
,………………………….2分
由正弦定理,得试题.files/image252.gif)
试题.files/image254.gif) ……………………………6分
……………………………6分
因此,试题.files/image256.gif)
试题.files/image258.gif) …………………………………………5分
…………………………………………5分
试题.files/image260.gif) .……………………………………………………………………2分
.……………………………………………………………………2分
[解二] 延长试题.files/image089.gif) 交地平线与
交地平线与试题.files/image263.gif) ,…………………………………………………………………3分
,…………………………………………………………………3分
由已知,得试题.files/image265.gif) …………………………………………………4分
…………………………………………………4分
整理,得试题.files/image104.gif) ………………………………………………………………………8分
………………………………………………………………………8分
17.[解](Ⅰ)函数试题.files/image110.gif) 的定义域为
的定义域为试题.files/image269.gif) …………………………………………………………2分
…………………………………………………………2分
试题.files/image271.gif) ,
,
当试题.files/image108.gif) 时,因为
时,因为试题.files/image274.gif) ,所以
,所以试题.files/image276.gif) ,
,
试题.files/image278.gif) ,从而
,从而试题.files/image280.gif) ,……………………………………………………..4分
,……………………………………………………..4分
所以函数试题.files/image110.gif) 的值域为
的值域为试题.files/image283.gif) .………………………………………………………………..1分
.………………………………………………………………..1分
(Ⅱ)假设函数试题.files/image110.gif) 是奇函数,则,对于任意的
是奇函数,则,对于任意的试题.files/image285.gif) ,有
,有试题.files/image287.gif) 成立,
成立,
即试题.files/image289.gif)
试题.files/image291.gif) 当
当试题.files/image293.gif) 时,函数
时,函数试题.files/image110.gif) 是奇函数.…………………………………………………………….3分
是奇函数.…………………………………………………………….3分
当试题.files/image108.gif) ,且
,且试题.files/image295.gif) 时,函数
时,函数试题.files/image110.gif) 是非奇非偶函数.………………………………………….1分
是非奇非偶函数.………………………………………….1分
试题.files/image297.gif) 对于任意的
对于任意的试题.files/image299.gif) ,且
,且试题.files/image301.gif) ,
,
试题.files/image303.gif)
试题.files/image305.gif)
试题.files/image307.gif) ……………………………………………..4分
……………………………………………..4分
试题.files/image291.gif) 当
当试题.files/image108.gif) 时,函数
时,函数试题.files/image110.gif) 是递减函数.………………………………………………..1分
是递减函数.………………………………………………..1分
18.[解](Ⅰ)因为试题.files/image122.gif) ,且
,且试题.files/image089.gif) 边通过点
边通过点试题.files/image310.gif) ,所以
,所以试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image313.gif) .1分
.1分
设试题.files/image115.gif) 两点坐标分别为
两点坐标分别为试题.files/image316.gif) .
.
由试题.files/image318.gif) 得
得试题.files/image320.gif) .
.
所以试题.files/image322.gif) . ……………………………………………..4分
. ……………………………………………..4分
又因为试题.files/image089.gif) 边上的高
边上的高试题.files/image093.gif) 等于原点到直线
等于原点到直线试题.files/image326.gif) 的距离.
的距离.
所以试题.files/image328.gif) ,
,试题.files/image330.gif) . ……………………………………….3分
. ……………………………………….3分
(Ⅱ)设试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image333.gif) , ……………………………………………..1分
, ……………………………………………..1分
由试题.files/image335.gif) 得
得试题.files/image337.gif) . …………………………………..2分
. …………………………………..2分
因为试题.files/image115.gif) 在椭圆上,所以
在椭圆上,所以试题.files/image340.gif) . ………………….. …………..1分
. ………………….. …………..1分
设试题.files/image115.gif) 两点坐标分别为
两点坐标分别为试题.files/image316.gif) ,
,
则试题.files/image344.gif) ,
,试题.files/image346.gif) ,
,
所以试题.files/image348.gif) .……………………………………………..3分
.……………………………………………..3分
又因为试题.files/image350.gif) 的长等于点
的长等于点试题.files/image352.gif) 到直线
到直线试题.files/image326.gif) 的距离,即
的距离,即试题.files/image355.gif) .……………..2分
.……………..2分
所以试题.files/image357.gif) .…………………..2分
.…………………..2分
所以当试题.files/image359.gif) 时,
时,试题.files/image131.gif) 边最长,(这时
边最长,(这时试题.files/image362.gif) )
)
此时试题.files/image089.gif) 所在直线的方程为
所在直线的方程为试题.files/image365.gif) . ……………………………………………..1分
. ……………………………………………..1分
17.[解](Ⅰ)由题意,试题.files/image367.gif) ……………………………6分
……………………………6分
(Ⅱ)解法1:由试题.files/image172.gif) 且
且试题.files/image178.gif) 知
知
试题.files/image370.gif) ,
,试题.files/image372.gif) ,
,试题.files/image374.gif)
试题.files/image376.gif) ,
,试题.files/image378.gif) ,
,试题.files/image380.gif)
因此,可猜测试题.files/image382.gif) (
(试题.files/image174.gif) ) ………………………………………………………4分
) ………………………………………………………4分
将试题.files/image382.gif) ,
,试题.files/image385.gif) 代入原式左端得
代入原式左端得
左端试题.files/image387.gif)
试题.files/image389.gif)
试题.files/image391.gif)
即原式成立,故试题.files/image382.gif) 为数列的通项.……………………………………………………….3分
为数列的通项.……………………………………………………….3分
用数学归纳法证明得3分
解法2:由 试题.files/image178.gif) ,
,试题.files/image176.gif)
令试题.files/image395.gif) 得
得试题.files/image397.gif) ,且
,且试题.files/image399.gif)
即试题.files/image401.gif) ,……… ……………………………………………………………..4分
,……… ……………………………………………………………..4分
所以试题.files/image403.gif)
因此试题.files/image405.gif) ,
,试题.files/image407.gif) ,...,
,...,试题.files/image409.gif)
将各式相乘得试题.files/image382.gif) ………………………………………………………………………………3分
………………………………………………………………………………3分
(Ⅲ)设上表中每行的公比都为试题.files/image412.gif) ,且
,且试题.files/image414.gif) .因为
.因为试题.files/image416.gif) ,
,
所以表中第1行至第9行共含有数列试题.files/image166.gif) 的前63项,故
的前63项,故试题.files/image418.gif) 在表中第10行第三列,………2分
在表中第10行第三列,………2分
因此试题.files/image420.gif) .又
.又试题.files/image422.gif) ,所以
,所以试题.files/image424.gif) .…………………………………..3分
.…………………………………..3分
则试题.files/image426.gif) .
.试题.files/image187.gif) …………………………………………2分
…………………………………………2分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com