
题目列表(包括答案和解析)
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数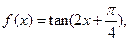 ,
,
(Ⅰ)求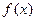 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设 ,若
,若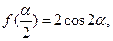 求
求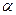 的大小.
的大小.
三、解答题:本大题共6小题,共80分.
15.(本小题满分13分)
已知函数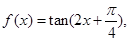 ,
,
(Ⅰ)求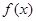 的定义域与最小正周期;
的定义域与最小正周期;
(Ⅱ)设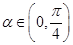 ,若
,若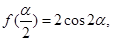 求
求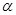 的大小.
的大小.
二、解答题:本大题共6小题,共90分。请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤。
15、(本小题满分14分)在△ABC中,角A、B、C所对应的边为
(1)若 求A的值;
求A的值;
(2)若 ,求
,求 的值.
的值.
箱子里有3双不同的手套,随机地拿出2只,记事件A={拿出的手套配不成对};事件B={拿出的都是同一只手上的手套};事件C={拿出的手套一只是左手的,一只是右手的,但配不成对}。(本小题满分13分)
(1)请罗列出所有的基本事件;
(2)分别求事件A、事件B、事件C的概率;
(3)说出事件A、事件B、事件C的关系。
【解析】第一问利用分别设3双手套为:
 ;
;
 ;
;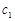
 。
。  、
、 、
、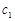 分别代表左手手套,
分别代表左手手套, 、
、 、
、 分别代表右手手套。
分别代表右手手套。
第二问①事件A包含12个基本事件,故P(A)= 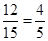 ,(或能配对的只有3个基本事件,
,(或能配对的只有3个基本事件,
P(A)= 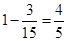 );
);
②事件B包含6个基本事件,故P(B)= 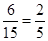 ;
;
事件C包含6个基本事件,故P(C)= 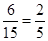
第三问
解:(1)分别设3双手套为:
 ;
;
 ;
;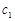
 。
。  、
、 、
、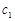 分别代表左手手套,
分别代表左手手套, 、
、 、
、 分别代表右手手套。…………2分
分别代表右手手套。…………2分
箱子里 的3双不同的手套,随机地拿出2只,所有的基本事件是:
( ,
, )、(
)、( ,
,
 )、(
)、( ,
, )、(
)、( ,
,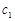 )、(
)、( ,
, )
)
( ,
, )、(
)、( ,
, )、(
)、( ,
,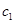 )、(
)、( ,
, );
);
( ,
, )、(
)、( ,
,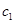 )、(
)、( ,
, )
)
( ,
,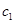 )、(
)、( ,
, )、(
)、(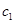 ,
, ) 共15个基本事件。 ……………5分
) 共15个基本事件。 ……………5分
(2)①事件A包含12个基本事件,故P(A)= 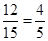 ,(或能配对的只有3个基本事件,
,(或能配对的只有3个基本事件,
P(A)= 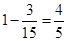 );
……………7分
);
……………7分
②事件B包含6个基本事件,故P(B)= 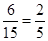 ;…………9分
;…………9分
③事件C包含6个基本事件,故P(C)= 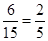 。…………11分
。…………11分
⑶ 
(本小题满分13分)2012年3月2日,国家环保部发布了新修订的《环境空气质量标准》.其中规定:居民区中的PM2.5年平均浓度不得超过35微克/立方米,PM2.5的24小时平均浓度不得超过75微克/立方米. 某城市环保部门随机抽取了一居民区去年40天的PM2.5的24小时平均浓度的监测数据,数据统计如下:
|
组别 |
PM2.5(微克/立方米) |
频数(天) |
频 率 |
|
第一组 |
(0,15] |
4 |
0.1 |
|
第二组 |
(15,30] |
12 |
|
|
第三组 |
(30,45] |
8 |
0.2 |
|
第四组 |
(45,60] |
8 |
0.2 |
|
第五组 |
(60,75] |
|
0.1 |
|
第六组 |
(75,90) |
4 |
0.1 |
(Ⅰ)试确定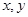 的值,并写出该样本的众数和中位数(不必写出计算过程);
的值,并写出该样本的众数和中位数(不必写出计算过程);
(Ⅱ)完成相应的频率分布直方图.
(Ⅲ)求出样本的平均数,并根据样本估计总体的思想,从PM2.5的年平均浓度考虑,判断该居民区的环境是否需要改进?说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com