
题目列表(包括答案和解析)
 (本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(本小题满分12分)如图所示,将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN,要求M在AB的延长线上,N在AD的延长线上,且对角线MN过C点。已知AB=3米,AD=2米。
(I)设![]() (单位:米),要使花坛AMPN的面积大于32平方米,求
(单位:米),要使花坛AMPN的面积大于32平方米,求![]() 的取值范围;
的取值范围;
(II)若![]() (单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(单位:米),则当AM,AN的长度分别是多少时,花坛AMPN的面积最大?并求出最大面积。
(本小题满分12分)
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米, 米.
米.
(1)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.
(本小题满分12分)
如图所示,将一矩形花坛 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛 ,要求
,要求 点在
点在 上,
上,  点在
点在 上,且对角线
上,且对角线 过点
过点 ,已知
,已知 米,
米,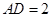 米.
米.
(1)要使矩形 的面积大于32平方米,则
的面积大于32平方米,则 的长应在什么范围内?
的长应在什么范围内?
(2)当 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛 的面积最小?并求出最小值.
的面积最小?并求出最小值.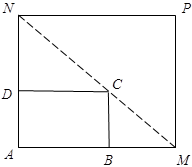
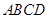 扩建成一个更大的矩形花坛
扩建成一个更大的矩形花坛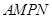 ,要求
,要求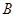 点在
点在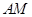 上,
上, 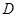 点在
点在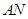 上,且对角线
上,且对角线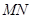 过点
过点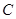 ,已知
,已知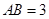 米,
米,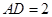 米.
米.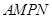 的面积大于32平方米,则
的面积大于32平方米,则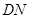 的长应在什么范围内?
的长应在什么范围内?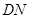 的长度为多少时,矩形花坛
的长度为多少时,矩形花坛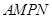 的面积最小?并求出最小值.
的面积最小?并求出最小值.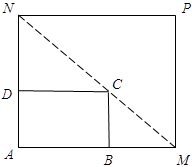
(本小题满分12分)
 如图所示,一辆汽车从
如图所示,一辆汽车从![]() 点出发,沿海岸线一条直线公路以100千米/小时的速度向东匀速行驶,汽车开动时,在距
点出发,沿海岸线一条直线公路以100千米/小时的速度向东匀速行驶,汽车开动时,在距![]() 点500千米,且与海岸线距离400千米的海面上
点500千米,且与海岸线距离400千米的海面上![]() 点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机。该快艇至少以多大的速度行驶,才能将物品送到汽车司机手中?并求出快艇所行驶的距离。
点处有一艘快艇与汽车同时出发,要把一件重要物品送给这辆汽车司机。该快艇至少以多大的速度行驶,才能将物品送到汽车司机手中?并求出快艇所行驶的距离。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com