
题目列表(包括答案和解析)
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分.)
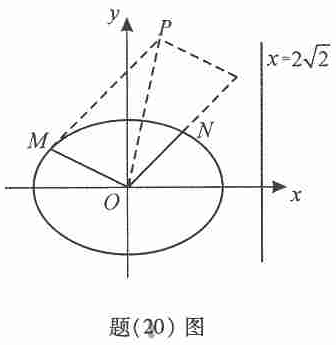
如题(20)图,椭圆的中心为原点![]() ,离心率
,离心率![]() ,一条准线的方程为
,一条准线的方程为![]() .
.
(Ⅰ)求该椭圆的标准方程;
(Ⅱ)设动点![]() 满足:
满足:![]() ,其中
,其中![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,问:是否存在两个定点
,问:是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分.)
已知函数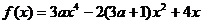
(Ⅰ)当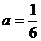 时,求
时,求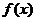 的极值与相应的
的极值与相应的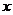 的值;
的值;
(Ⅱ)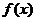 在
在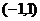 上不是增函数,求
上不是增函数,求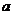 的取值范围.
的取值范围.
(本小题满分12分)
某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5; 第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案,第二年与第一年相互独立。令![]() 表示方案
表示方案![]() 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。
(1)写出![]() 的分布列;
的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到灾前产量,预计可带来效益10万元;两年后柑桔产量恰好达到灾前产量,预计可带来效益15万元;柑桔产量超过灾前产量,预计可带来效益20万元;问实施哪种方案所带来的平均效益更大?
(本小题满分12分)
某柑桔基地因冰雪灾害,使得果林严重受损,为此有关专家提出两种拯救果林的方案,每种方案都需分两年实施;若实施方案一,预计当年可以使柑桔产量恢复到灾前的1.0倍、0.9倍、0.8倍的概率分别是0.3、0.3、0.4;第二年可以使柑桔产量为上一年产量的1.25倍、1.0倍的概率分别是0.5、0.5. 若实施方案二,预计当年可以使柑桔产量达到灾前的1.2倍、1.0倍、0.8倍的概率分别是0.2、0.3、0.5;第二年可以使柑桔产量为上一年产量的1.2倍、1.0倍的概率分别是0.4、0.6. 实施每种方案,第二年与第一年相互独立。令 表示方案
表示方案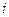 实施两年后柑桔产量达到灾前产量的倍数。
实施两年后柑桔产量达到灾前产量的倍数。
(1)写出 的分布列;
的分布列;
(2)实施哪种方案,两年后柑桔产量超过灾前产量的概率更大?
(3)不管哪种方案,如果实施两年后柑桔产量达不到灾前产量,预计可带来效益10万元;两年后柑桔产量恰好达到灾前产量,预计可带来效益15万元;柑桔产量超过灾前产量,预计可带来效益20万元;问实施哪种方案所带来的平均效益更大?
(本小题满分12分)探究函数 的最小值,并确定取得最小值时x的值.列表如下:
的最小值,并确定取得最小值时x的值.列表如下:
|
x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
|
y |
… |
16 |
10 |
8.34 |
8.1 |
8.01 |
8 |
8.01 |
8.04 |
8.08 |
8.6 |
10 |
11.6 |
15.14 |
… |
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数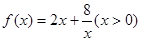 在区间(0,2)上递减;函数
在区间(0,2)上递减;函数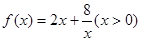 在区间 上递增.当
在区间 上递增.当 时,
时, .
.
(2)证明:函数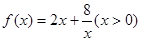 在区间(0,2)递减.
在区间(0,2)递减.
(3)思考:函数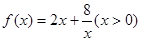 时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com