练习册

  • 练习册
  • 试题
    如图6-2所示.将金属丝AB弯成半径r＝1 m的圆弧.但是AB之间留出宽度为d＝2 cm.相对于圆弧来说很小的间隙.电荷量Q＝3.14×10-9 C的正电荷均匀分布在金属丝上.求圆心O处的电场强度． 图6-2 [解析] 设原缺口环所带电荷的线密度为ρ.则ρ＝≈ 补上的金属小段的带电荷量Q′＝ρd＝ 将Q′视为点电荷(因为d≪r).它在O处的场强为 E1＝＝9×10-9×× N/C ＝9×10-20 N/C 设要求的场强为E2.由E1+E2＝0可得 E2＝-E1＝-9×10-20 N/C.负号表示E2方向与E1方向相反.向左． [答案] 9×10-20 N/C 方向向左 巧用比例法处理电场中的平衡问题 所谓比例法.就是根据物理规律.公式.已知两个物理量的变化成正比或反比.当一个或几个物理量变化时.可以利用这种正比或反比的规律.确定某个物理量的变化.这种方法比起直接计算.数值运算少.速度快．但在应用此法时.必须理解物理公式中哪些是变量.哪些是不变量.研究的物理问题中涉及的物理量是什么关系等问题.并能将多个公式连续应用比例法分析问题． (2014·杭州外国语学校模拟)质量为m1.m2的小球分别带同种电荷q1和q2.它们用等长的细线吊在同一点O.由于静电斥力的作用.使小球m1靠在竖直光滑墙上.m1的拉线l1呈竖直方向.使小球m2的拉线l2与竖直方向成θ角.m1.m2均处于静止状态.如图6-3所示． 图6-3 由于某种原因.小球m2带的电荷量q2逐渐减少.于是两球拉线之间夹角θ也逐渐减小直到零．在θ角逐渐减小的过程中.关于l1.l2中的张力T1.T2的变化是( ) A．T1不变.T2不变 B．T1不变.T2变小 C．T1变小.T2变小 D．T1变小.T2不变 [解析] 以小球m2为研究对象.受力如图所示．由几何关系易得.力的矢量三角形BG2T′2与三角形OAB相似.由对应边成比例可得.F∶lAB＝G2∶l1＝T′2∶l2.小球m2处于平衡状态.则有T2＝T′2.由库仑定律得:F＝k.小球m2受到的重力为:G2＝m2g.解得:T2＝T′2＝.由于l1.l2不变.所以T2不变, F＝.由于lAB逐渐减小.所以F逐渐减小．由小球m1的平衡方程可得:T1＝m1g+Fcos＝m1g+Fsin .由于F.θ都减小.所以T1变小.A.B.C错误.D正确． [答案] D [即学即用] 【查看更多】

     

    题目列表(包括答案和解析)

    如图13-11-1所示，将金属丝AB弯成半径r=1 m的圆弧，但在A、B之间留出宽度为d=2 cm、相对来说很小的间隙.将电荷量Q=3.13×10-9C的正电荷均匀分布在金属丝上.求圆心O处的电场强度.

    图13-11-1

       

    查看答案和解析>>

    (10分)如图所示，用金属丝AB弯成半径r=l m的圆弧，但在A、B之间留出宽度为d=2 cm相对来说很小的间隙．将电量q=3.13×10-9C的正电荷均匀分布金属丝上，求圆心O处的电场强度．

    查看答案和解析>>

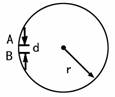
     如图1所示，将细金属丝AB弯成半径R＝0.5m的缺口圆环，在A、B两端处留有宽度d=1cm的间隙.现将总电荷量Q＝3.13×10-19C的正电荷均匀分布在金属丝上，求圆心O点处的电场强度.

    查看答案和解析>>

    如图1所示，用金属丝AB弯成半径为r=1.0m的圆弧，在A、B之间留有宽度d=2cm的间隙.将电量Q=3.13×10-9C的正电荷均匀分布于金属丝上.求圆心O处的电场强度.

    查看答案和解析>>

    在“测定金属丝的电阻率”的实验中，需要用刻度尺测出金属丝的长度l，用螺旋测微器测出金属丝的直径d，用电流表和电压表测出金属丝的电阻R．
    精英家教网
    （1）实验中测量金属丝的长度和直径时，刻度尺和螺旋测微器的示数分别如图1、2所示，则金属丝长度的测量值l=
     
    cm，金属丝直径的测量值为d=
     
    mm．
    （2）实验中给定电压表（内电阻为50kΩ）、电流表（内电阻为40Ω）、滑动变阻器（最大阻值为10Ω）、待测金属丝（电阻约为100Ω）、电源、开关及导线若干．两位同学想用伏安法多次测量做出I-U图线求出待测金属丝的阻值，他们设计了图3甲、乙两个电路，你认为采用
     
    图更合理（填“甲”或“乙”），电压表的右端应接在
     
    点（填“a”或“b”）．
    （3）请你用笔画线代替导线，在图4中按照第（2）问你所选择的电路图连接实验电路．
    （4）用正确的方法测出了多组电流和电压值，并标在I-U坐标系中，如图5中“×”所示．请你根据测量值画出图线，并求出金属丝的阻值Rx=
     
    Ω．则这种金属的电阻率约为
     
    Ω?m（该结果保留一位有效数字）．

    查看答案和解析>>


    同步练习册答案