
题目列表(包括答案和解析)
已知函数![]() 是定义域为R的偶函数,其图像均在x轴的上方,对任意的
是定义域为R的偶函数,其图像均在x轴的上方,对任意的![]() ,都有
,都有![]() ,且
,且![]() ,又当
,又当![]() 时,其导函数
时,其导函数![]() 恒成立。
恒成立。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)解关于x的不等式: ,其中
,其中![]()
已知函数 是定义域为R的偶函数,且
是定义域为R的偶函数,且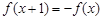 ,若
,若 在
在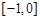 上是增函数,那么
上是增函数,那么 在
在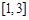 上是
上是
A.增函数 B.减函数 C.先增后减的函数 D.先减后增的函数
已知函数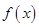 是定义域为R的偶函数,且
是定义域为R的偶函数,且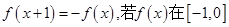 上是增函数,那么
上是增函数,那么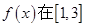 上是( )
上是( )
A.增函数 B.减函数 C.先增后减的函数 D.先减后增的函数
已知函数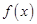 是定义域为R的偶函数,且
是定义域为R的偶函数,且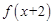 =
=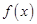 ,若
,若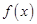 在
在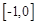 上是减函数,那么
上是减函数,那么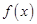 在
在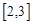 上是( )
上是( )
A.增函数 B.减函数
C.先增后减的函数 D.先减后增的函数
已知函数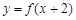 是定义域为R的偶函数,且当
是定义域为R的偶函数,且当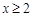 时,
时,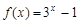 ,则当
,则当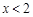 时,
时,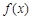 的解析式为( )
的解析式为( )
A.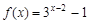 B.
B.  C.
C.
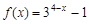 D.
D.
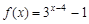
一、选择题:
1.C 2.B 3.A 4.D 5.C 6.B 7.A 8.C 9.A 10.D 11.D 12.B
二、填空题:
13.{―1} 14.0 15.45° 16.8/3 17.4
18.如2,6,18,54等 19.(0,3/2] 20 ..files/image148.gif)
21..files/image075.gif) 22.2y-3x+3=0 23.I ≤98,或I<100等
22.2y-3x+3=0 23.I ≤98,或I<100等
24.(1,8.2) 25..files/image149.gif) 26. ①③
26. ①③
三、解答题:
27解:(1)由.files/image151.gif)
.files/image153.gif) , 又
, 又.files/image155.gif) ,
,
.files/image157.gif)
(2).files/image159.gif)
.files/image161.gif)
同理:.files/image163.gif) ,
,
.files/image165.gif) ,
,
.files/image167.gif) ∴0<x<
∴0<x<.files/image169.gif)
.files/image171.jpg) 故
故.files/image173.gif) ,
,.files/image175.gif) ,
,.files/image177.gif) ..
..
28解法一:(1)F为PA的中点。下面给予证明:
延长DE、AB交于点M,由E为BC中点,知B为AM的中点,
连接BF,则BF∥PM,PM.files/image179.gif) 平面PDE,∴BF∥平面PDE。
平面PDE,∴BF∥平面PDE。
(2)DE为正△BCD的边BC上的中线,因此DE⊥BC,∴DE⊥AD,
又PA⊥平面ABCD,即 DE⊥PA, 所以 DE⊥平面PAD.
由此知平面PDE⊥平面PAD.
作AH⊥PD于H,则AH⊥平面PDE.
作HO⊥PM于O,
则∠AOH为所求二面角的平面角,
又在Rt∆PAD中∠PDA = 45°,PA = AD = 2,
因此AH =.files/image018.gif) ,又AO =
,又AO =.files/image182.gif) ,HO=
,HO=
.files/image184.gif)
.files/image186.gif)
解法二:以AD为X正半轴,AP为Z轴,建立空间坐标系,
则F(0,0,a),B(1,.files/image188.gif) ,P(0,0,2),D(2,0,0),E(2,
,P(0,0,2),D(2,0,0),E(2,.files/image188.gif)
.files/image191.gif) ,
,.files/image193.gif) ,令
,令.files/image195.gif)
.files/image197.gif) 面PDE,
面PDE,
.files/image199.gif)
因为BF∥面PDE, ∴-1+a=0, ∴a=1, ∴F(0,0,1)
(2)作DG⊥AB,可得G(.files/image201.gif) ),∵PA⊥面ABCD,∴PA⊥DG,又因为AB
),∵PA⊥面ABCD,∴PA⊥DG,又因为AB.files/image203.gif) AP=A,
AP=A,
∴DG⊥平面PAB, 设平面PDE与平面PAB所成的锐二面角为.files/image205.gif) ,
,
.files/image207.gif) =(
=(.files/image209.gif) ,所以tan
,所以tan.files/image205.gif) =
=.files/image212.gif) .
.
29解: (1)由题意知,.files/image107.gif) 的可能取值为0,1,2,3,且
的可能取值为0,1,2,3,且
.files/image215.gif) ,
,.files/image217.gif) ,
,
.files/image219.gif) ,
,.files/image221.gif) , 所以
, 所以.files/image107.gif) 的分布列为:
的分布列为:
.files/image107.gif)
.files/image225.gif)
.files/image227.gif)
.files/image229.gif)
.files/image231.gif)
.files/image233.gif)
.files/image235.gif)
.files/image237.gif)
.files/image090.gif)
.files/image240.gif)
.files/image242.gif) .
.
(2) 记“取出的这个球是白球”为事件.files/image244.gif) ,“从甲盒中任取
,“从甲盒中任取.files/image229.gif) 个球”为事件
个球”为事件.files/image247.gif) ,
,
.files/image249.gif) {从甲盒中任取
{从甲盒中任取.files/image229.gif) 个球均为红球},
个球均为红球},.files/image251.gif) {从甲盒中任取
{从甲盒中任取.files/image229.gif) 个球为一红一白},
个球为一红一白},
.files/image253.gif) {从甲盒中任取
{从甲盒中任取.files/image229.gif) 个球均为白球},显然
个球均为白球},显然.files/image255.gif) ,且
,且.files/image257.gif) 彼此互斥.
彼此互斥.
.files/image259.gif)
.files/image261.gif)
.files/image263.gif) .
.
30解:(1)
当a=1时,f(x)= .files/image265.gif) .
..files/image267.gif)
因此,曲线y=f(x)在点(2,f(2))处的切线方程为:5x-y-8=0…3分
(2)
x∈(0,2]时, f(x)= .files/image269.gif)
.files/image271.gif)
若2≤a<6,则.files/image273.gif) =0在(0,2)上有根x=
=0在(0,2)上有根x=.files/image275.gif) ,且在(0,
,且在(0,.files/image275.gif) )上
)上
.files/image273.gif) >0,在(
>0,在(.files/image275.gif) ,2)上
,2)上.files/image273.gif) <0, 因此, f(x)在x=
<0, 因此, f(x)在x=.files/image275.gif) 处取极大值,
处取极大值,
由于只有一个极值点,所以极大值也是最大值. 由此得.files/image279.gif) .
.
若a≥6,则在(0,2)上.files/image273.gif) >0,因此,f(x)在x∈(0,2]时单调递增,
>0,因此,f(x)在x∈(0,2]时单调递增,
∴当 x=2时f(x)最大,即2(2-a).files/image281.gif) =8∴a=0或4 ,均不合,舍去.
=8∴a=0或4 ,均不合,舍去.
综上知 a=.files/image283.gif) .
.
(3) x<0时,f(x)= .files/image285.gif) ,
,.files/image287.gif) <0.
<0.
f(x)单调递减,由k<0时,f(k-.files/image289.gif) )≤f(-
)≤f(-.files/image291.gif) )对任意的x≥0恒成立,
)对任意的x≥0恒成立,
知:k-.files/image289.gif) ≥-
≥-.files/image291.gif) 对任意的x≥0恒成立,即
对任意的x≥0恒成立,即.files/image293.gif) 对任意的x≥0
对任意的x≥0
恒成立,易得.files/image295.gif) 的最大值为0.
的最大值为0.
.files/image297.gif) .
.
31解:(1)由.files/image299.gif) 得
得
.files/image301.gif) ,
,
(2)
.files/image303.gif) ,
,
所以数列.files/image305.gif) 是以-2为首项,
是以-2为首项,.files/image022.gif) 为公比的等比数列,
为公比的等比数列,
.files/image308.gif) ,
,
.files/image310.gif) ,
,
.files/image312.gif) ,
,
.files/image314.gif) ,
,
(3) 假设存在整数m、n,使.files/image316.gif) 成立,则
成立,则.files/image318.gif) ,
,
因为.files/image320.gif)
只要.files/image322.gif)
又.files/image324.gif) ,因此m只可能为2或3,
,因此m只可能为2或3,
当m=2时,n=1显然成立。n≥2有.files/image326.gif) 故不合.
故不合.
当m=3时,n=1,.files/image328.gif) 故不合。n=2符合要求。
故不合。n=2符合要求。
n≥3,.files/image330.gif) 故不合。
故不合。
综上可知:m=2,n=1或m=3, n=2。
.files/image331.gif) 32解:(1)设A
32解:(1)设A.files/image333.gif) 、B
、B.files/image335.gif) ,直线的斜率为k.则由
,直线的斜率为k.则由 .files/image337.gif)
得x2-4kx-4b=0 ,
.files/image339.gif)
.files/image341.gif)
.files/image343.gif)
而b>0,∴b=4.
(2)以A、B为切点的抛物线的切线分别为
.files/image345.gif) ① ,
① ,
.files/image347.gif) ②
②
①÷②得.files/image349.gif) ③ 又
③ 又.files/image351.gif) 代入③
代入③
有.files/image353.gif)
.files/image355.gif)
即所求M点的轨迹方程为y=-4,
(3)假设存在直线y=a,被以AB为直径的圆截得的弦长为定值ℓ,
圆心距d=.files/image357.gif) ,
,
.files/image359.gif)
由ℓ为定值,所以a=-1
而当a=-1时,.files/image361.gif) =-9 ,因此a=-1不合题意,舍去。
=-9 ,因此a=-1不合题意,舍去。
故符合条件的直线不存在。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com