题目列表(包括答案和解析)
已知向量
＝(cosα，sinα)，
＝(cosβ，sinβ)，|
|＝
(1)求cos(α－β)的值；
(2)若－
＜β＜0＜α＜
，sinβ＝－
，求sinα的值．
已知向量＝(cos
，sin
)，＝(cos
，－sin
)，
，
(1)求证：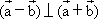
；
(2)|＋|＝
，求cosx的值．
已知向量
＝(cosα，sinα)，
＝(cosβ，sinβ)，|－|＝
．
(1)求cos(α－β)的值；
(2)若0＜α＜
，－
＜α＜0，且sinβ＝－
，求sinα的值
已知向量
＝(cosα，2)，
＝(sinα，1)且∥，则tan(α－45°)＝________．
已知向量
＝(cosα，sinα)，
＝(cosβ，sinβ)，
(1)求cos(α－β)的值；
(2)若－
＜β＜0＜α＜
，sinβ＝－
，求sinα的值．
一、 选择题：CACDA,ADCBB.
二、
填空题：11.（-4，2） 12.
13.-4 14. 12
15. 
三、解答题（16～18题，每题13分，19-21题12分，共75分）
16．解：∵
∴
∴
17.证明一：（利用共线向量的判定定理证明）
以
作为基底，有：
, 
，从而
, 所以A、E、F共线。
证明二：（利用三点共线的判定定理证明）
，而：
，所以A、E、F共线。
（可以建立坐标系，利用求出等比分点坐标公式求出E、F的坐标，再证明A、E、F共线）
18．（1）f(x)＝
sin2x－
(1＋cos2x)＋ ＝ sin2x－cos2x
＝sin(2x－
) 5分
∴T＝
＝π 2分
（2）函数y＝f(x)的图象按
＝（φ，0）（φ>0）平移后，得y＝sin(2(x－φ)－) 2分，此函数图象对称轴方程为2(x－φ)－＝kπ＋
k∈Z ，又f(x)平移后关于y轴对称，∴x＝0满足上式有2(0－φ)－＝kπ＋，∴φ＝－
π－
k∈Z
2分
∵φ>0∴当k＝－1时，φmin＝ 2分
19．（1）由已知得
－
＝(sinθ，2)－(－2，co sθ)＝(sinθ＋2，2－cosθ) 1分 ∵⊥－
∴?(－)＝0
∴(cosθ，sinθ)(sinθ＋2，2－cosθ)＝0
∴cosθ(sinθ＋2)＋sinθ(2－cosθ)＝0 2分
∴2cosθ＋2sinθ＝0 ∴tanθ＝－1 ∵θ∈（－π，π）
∴θ＝－
或θ＝
3分
（2）由已知
＝＋－＝(cosθ＋sinθ＋2，sinθ＋2－cosθ) 1分
∴||2＝(cosθ＋sinθ＋2)2＋(sinθ＋2－cosθ)2＝10＋8sinθ 2分
∵||≤
∴10＋8sinθ≤14 ∴sinθ≤ ∵θ∈(－π，π)
∴θ∈
3分
20．轮船从点C到点B耗时60分钟，从点B到点E耗时20分钟，而船始终匀速，可见BC＝3EB
2分
设EB＝x，则BC＝3x，由条件知∠BAE＝60°，在△ABE中，由正弦定理得
①
在△ABC中，由正弦定理得 
②
2分
由条件∠BAC＝30°＋30°＝60° ∴sin∠BAC＝sin∠BAE
又∠ABC＋∠ABE＝180° ∴sin∠BAC＝sin(180°－∠ABC)＝sin∠ABE 2分
结合①②得
＝
∴AC＝3AE 2分
在△ACE中，由余弦定理，得
CE2＝AC2＋AE2－2AC?AE?cos120°＝9AE2＋AE2＋3AE2＝13AE2＝13×
∴CE＝20 2分 ∴BC＝15 ∴船速v＝15km/t 2分
21.解： 可以组建命题一：△ABC中，若a、b、c成等差数列，求证：（1）0＜B≤
（2）
；
命题二：△ABC中，若a、b、c成等差数列求证：（1）0＜B≤
（2）1＜
≤
命题三：△ABC中，若a、b、c成等差数列，求证：（1）
（2）1＜
≤
命题四：△ABC中，若a、b、c成等比数列，求证：（1）0＜B≤
（2）1＜≤
………………………………………………………………………………………………6分
下面给出命题一、二、三的证明：
（1）∵a、b、c成等差数列∴2b=a+c，∴b=
≥
且B∈（0，π），∴0＜B≤
（2）
（3）
∵0＜B≤ ∴
∴
∴
下面给出命题四的证明：
（4）∵a、b、c成等比数列∴b2=a+c，
且B∈（0，π），∴0＜B≤…14分
评分时若构建命题的结论仅一个但给出了正确证明，可判7分；若构建命题完全正确但论证仅正确给出一个，可判10分；若组建命题出现了错误，应判0分，即坚持错不得分原则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com