
题目列表(包括答案和解析)
已知函数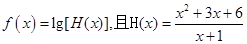 ,
,
(1)求函数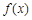 的定义域;
的定义域;
(2)求函数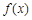 在区间
在区间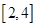 上的最小值;
上的最小值;
(3)已知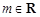 ,命题p:关于x的不等式
,命题p:关于x的不等式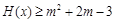 对函数
对函数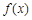 的定义域上的任意
的定义域上的任意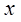 恒成立;命题q:指数函数
恒成立;命题q:指数函数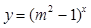 是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
是增函数.若“p或q”为真,“p且q”为假,求实数m的取值范围.
【解析】第一问中,利用由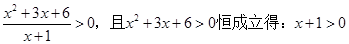 即
即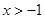
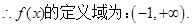
第二问中,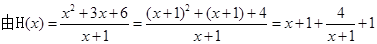 ,
,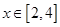 得:
得:
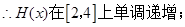
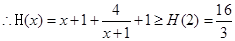 ,
,
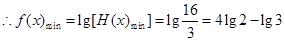
第三问中,由在函数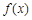 的定义域上
的任意
的定义域上
的任意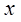 ,
,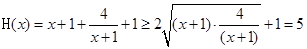 ,当且仅当
,当且仅当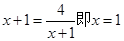 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,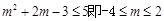 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时;当命题p为假,命题q为真时分为两种情况讨论即可 。
解:(1)由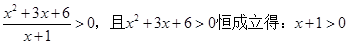 即
即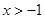
(2)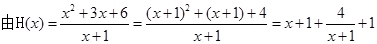 ,
,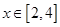 得:
得:
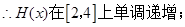
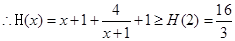 ,
,
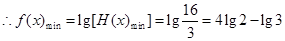
(3)由在函数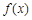 的定义域上
的任意
的定义域上
的任意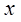 ,
,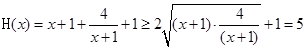 ,当且仅当
,当且仅当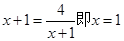 时等号成立。当命题p为真时,
时等号成立。当命题p为真时,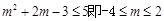 ;而命题q为真时:指数函数
;而命题q为真时:指数函数 .因为“p或q”为真,“p且q”为假,所以
.因为“p或q”为真,“p且q”为假,所以
当命题p为真,命题q为假时,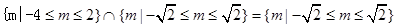
当命题p为假,命题q为真时,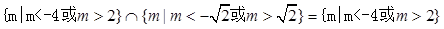 ,
,
所以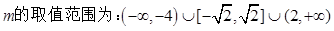
我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径,“开立圆术”相当于给出了已知球的体积V,求其直径d的一个近似公式![]() 。人们还用过一些类似的近似公式。根据
。人们还用过一些类似的近似公式。根据![]() =3.14159…..判断,下列近似公式中最精确的一个是
=3.14159…..判断,下列近似公式中最精确的一个是
![]()
如图,长方体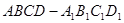 中,底面
中,底面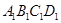 是正方形,
是正方形,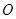 是
是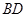 的中点,
的中点,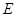 是棱
是棱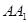 上任意一点。
上任意一点。
(Ⅰ)证明: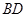
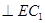 ;
;
(Ⅱ)如果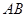 =2 ,
=2 ,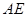 =
=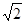 ,
,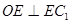 , 求
, 求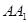 的长。
的长。
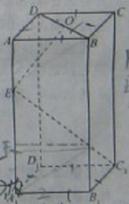
【解析】(Ⅰ)因底面是正方形,故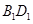
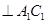 ,又侧棱垂直底面,可得
,又侧棱垂直底面,可得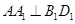 ,而
,而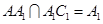 ,所以
,所以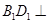 面
面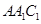 ,因
,因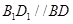 ,所以
,所以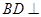 面
面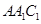 ,又
,又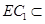 面
面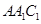 ,所以
,所以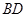
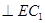 ;
;
(Ⅱ)因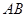 =2 ,
=2 ,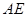 =
=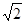 ,,可得
,,可得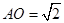 ,
,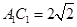 ,设
,设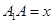 ,由
,由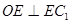 得
得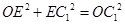 ,即
,即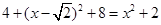 ,解得
,解得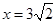 ,即
,即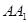 的长为
的长为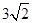 。
。
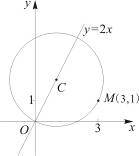
求圆心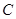 在直线
在直线 上,且经过原点及点
上,且经过原点及点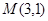 的圆
的圆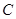 的标准方程.
的标准方程.
【解析】本试题主要考查的圆的方程的求解,利用圆心和半径表示圆,首先设圆心C的坐标为( ),然后利用
),然后利用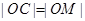 ,得到
,得到 ,从而圆心
,从而圆心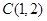 ,半径
,半径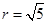 .可得原点 标准方程。
.可得原点 标准方程。
解:设圆心C的坐标为( ),...........2分
),...........2分
则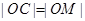 ,即
,即
 ,解得
,解得 ........4分
........4分
所以圆心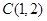 ,半径
,半径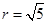 ...........8分
...........8分
故圆C的标准方程为: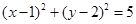 .......10分
.......10分
在 中,
中, 是三角形的三内角,
是三角形的三内角,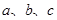 是三内角对应的三边,已知
是三内角对应的三边,已知 成等差数列,
成等差数列,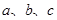 成等比数列
成等比数列
(Ⅰ)求角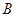 的大小;
的大小;
(Ⅱ)若 ,求
,求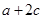 的值.
的值.
【解析】第一问中利用依题意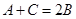 且
且 ,故
,故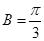
第二问中,由题意 又由余弦定理知
又由余弦定理知
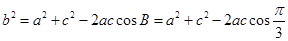
,得到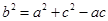 ,所以
,所以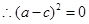 ,从而得到结论。
,从而得到结论。
(1)依题意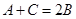 且
且 ,故
,故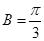 ……………………6分
……………………6分
(2)由题意 又由余弦定理知
又由余弦定理知
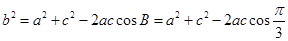 …………………………9分
…………………………9分
即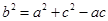 故
故
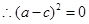
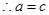 代入
代入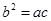 得
得

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com