
题目列表(包括答案和解析)
蜜蜂蜂房是严格的六角柱状体,它的一端是平整的六角形开口,另一端是封闭的六角菱锥形的底,由三个相同的菱形组成.组成底盘的菱形的钝角为109度28分,所有的锐角为70度32分,这样既坚固又省料.蜂房的巢壁厚0.073毫米,误差极小.
丹顶鹤总是成群结队迁飞,而且排成“人”字形.“人”字形的角度是110度.更精确地计算还表明“人”字形夹角的一半——即每边与鹤群前进方向的夹角为54度44分8秒!而金刚石结晶体的角度正好也是54度44分8秒!是巧合还是某种大自然的“默契”?
蜘蛛结的“八卦”形网,是既复杂又美丽的八角形几何图案,人们即使用直尺的圆规也很难画出像蜘蛛网那样匀称的图案.
冬天,猫睡觉时总是把身体抱成一个球形,这其间也有数学,因为球形使身体的表面积最小,从而散发的热量也最少.
真正的数学“天才”是珊瑚虫.珊瑚虫在自己的身上记下“日历”,它们每年在自己的体壁上“刻画”出365条斑纹,显然是一天“画”一条.奇怪的是,古生物学家发现3亿5千万年前的珊瑚虫每年“画”出400幅“水彩画”.天文学家告诉我们,当时地球一天仅21.9小时,一年不是365天,而是400天.
1.同学们,大自然中有许多有关数学的奥妙,许多现象有意无意地应用着数学,对于这些现象你有什么看法吗?请你谈谈你对大自然中的数学现象的认识.
2.把你发现的大自然中的数学问题告诉你的同学和老师,让他们也分享一下你认识大自然的乐趣.
如图,已知圆锥体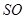 的侧面积为
的侧面积为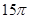 ,底面半径
,底面半径 和
和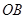 互相垂直,且
互相垂直,且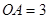 ,
,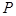 是母线
是母线 的中点.
的中点.

(1)求圆锥体的体积;
(2)异面直线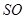 与
与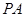 所成角的大小(结果用反三角函数表示).
所成角的大小(结果用反三角函数表示).
【解析】本试题主要考查了圆锥的体积和异面直线的所成的角的大小的求解。
第一问中,由题意,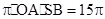 得
得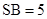 ,故
,故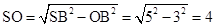
从而体积 .2中取OB中点H,联结PH,AH.
.2中取OB中点H,联结PH,AH.
由P是SB的中点知PH//SO,则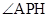 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO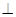 平面OAB,
平面OAB,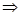 PH
PH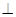 平面OAB,PH
平面OAB,PH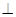 AH.在
AH.在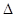 OAH中,由OA
OAH中,由OA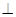 OB得
OB得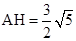 ;
;
在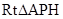 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2,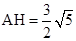 ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
解:(1)由题意,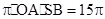 得
得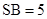 ,
,
故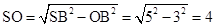 从而体积
从而体积 .
.
(2)如图2,取OB中点H,联结PH,AH.
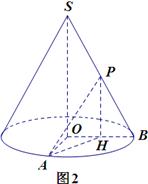
由P是SB的中点知PH//SO,则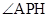 (或其补角)就是异面直线SO与PA所成角.
(或其补角)就是异面直线SO与PA所成角.
由SO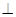 平面OAB,
平面OAB,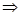 PH
PH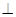 平面OAB,PH
平面OAB,PH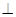 AH.
AH.
在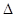 OAH中,由OA
OAH中,由OA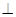 OB得
OB得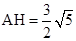 ;
;
在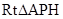 中,
中, ,PH=1/2SB=2,
,PH=1/2SB=2,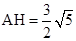 ,
,
则 ,所以异面直线SO与P成角的大arctan
,所以异面直线SO与P成角的大arctan
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com