练习册

  • 练习册
  • 试题
    (2012.威海.数形结合思想.反证法)如图13.在平面直角坐标系中.抛物线的顶点为B(2.1).且过点A(0.2).直线y=x与抛物线交于点D,E(点E在对称轴的右侧).抛物线的对称轴交直线y=x于点C.交x轴于点G.EF⊥x轴.垂足为点F.点P在抛物线上.且位于对称轴的右侧.PM⊥x轴.垂足为点M.△PCM为等边三角形. (1)求该抛物线的表达式, 图13 (2)求点P的坐标, (3)试判断CE与EF是否相等.并说明理由, (4)连结PE.在x轴上点M的右侧是否存在一点N.使△CMN与△CPE全等?若存在.试求出点N的坐标,若不存在.请说明理由. 【查看更多】

     

    题目列表(包括答案和解析)

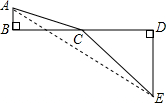    （2012•青田县模拟）为了探索代数式
    		x2+1
    +
    		(8-x)2+25
    的最小值，小明巧妙的运用了“数形结合”思想．具体方法是这样的：如图，C为线段BD上一动点，分别过点B、D作AB⊥BD，ED⊥BD，连接AC、EC．已知AB=1，DE=5，BD=8，设BC=x．则AC=
    		x2+1
    ，CE=
    		(8-x)2+25
    ，则问题即转化成求AC+CE的最小值．
    （1）我们知道当A、C、E在同一直线上时，AC+CE的值最小，于是可求得
    		x2+1
    +
    		(8-x)2+25
    的最小值等于
    10
    10
    ，此时x=
    4
    3
    4
    3
    ；
    （2）请你根据上述的方法和结论，试构图求出代数式
    		x2+4
    +
    		(12-x)2+9
    的最小值．

    查看答案和解析>>

    阅读并解答下面问题：
    （1）如图所示，直线l的两侧有A、B两点，在l上求作一点P，使AP+BP的值最小．（要求尺规作图，保留作图痕迹，不写画法和证明）
    （2）如图A、B两个化工厂位于一段直线形河堤的同侧，A工厂至河堤的距离AC为1km，B工厂到河堤的距离BD为2km，经测量河堤上C、D两地间的距离为6km．现准备在河堤边修建一个污水处理厂，为使A、B两厂到污水处理厂的排污管道最短，污水处理厂应建在距C地多远的地方？
    （3）通过以上解答，充分展开联想，运用数形结合思想，请你尝试解决下精英家教网面问题：若y=
    		x2+1
    +
    		(9-x)2+4
    ，当x为何值时，y的值最小，并求出这个最小值．

    查看答案和解析>>

    点A、B在数轴上分别表示有理数a、b，A、B两点之间的距离表示为AB，在数轴上A、B两点之间的距离AB=|a-b|．
    利用数形结合思想回答下列问题：
    （1）如果点A表示数5，将点A先向左移动4个单位长度，再向右移动7个单位长度，那么终点B表示的数是
    8
    8
    ，A、B两点间的距离是
    3
    3
    ；
    （2）数轴上表示1和-3的两点之间的距离是
    4
    4
    ；
    （3）数轴上表示x和1的两点之间的距离是
    |x-1|
    |x-1|
    ；
    （4）若x表示一个有理数，且|x-1|+|x+3|=4，则x的取值范围是
    -3≤x≤1
    -3≤x≤1
    ．

    查看答案和解析>>

    探索性问题
    已知A，B在数轴上分别表示a、b．
    利用数形结合思想回答下列问题：
    （1）填写下表：
    数 列A 列B 列C 列D 列E 列F
    a 5 -5 -6 -6 -10 -2.5
    b 3 0 4 -4 2 -2.5
    A，B两点的距离
    （2）任取上表一列数，你发现距离表示列式为
    列A=|5-3|=2
    列A=|5-3|=2
    ，则数轴上表示x和-2的两点之间的距离表示为
    |x+2|
    |x+2|
    ．
    （3）若x表示一个有理数，且-3＜x＜1，则|x-1|+|x+3|=
    4
    4
    ．
    （4）若A，B两点的距离为d，则d与a、b有何数量关系．

    查看答案和解析>>

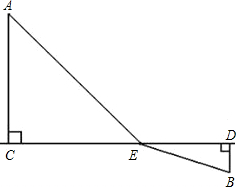    如图，A，B两个工厂位于一段直线形河的异侧，A厂距离河边AC=5km，B厂距离河精英家教网边BD=1km，经测量CD=8km，现准备在河边某处（河宽不计）修一个污水处理厂E．
    （1）设ED=x，请用x的代数式表示AE+BE的长；
    （2）为了使两厂的排污管道最短，污水厂E的位置应怎样来确定此时需要管道多长？
    （3）通过以上的解答，充分展开联想，运用数形结合思想，请你猜想
    		x2+4
    +
    		(12-x)2+9
    的最小值为
     
    ．

    查看答案和解析>>


    同步练习册答案