练习册

  • 练习册
  • 试题
    如图, 正方体ABCD-A1B1C1D1的棱长为1, P为BC的中点, Q为线段CC1上的动点, 过点A, P, Q的平面截该正方体所得的截面记为S. 则下列命题正确的是 (写出所有正确命题的编号). ①当0< CQ< 时, S为四边形 ②当CQ=时, S为等腰梯形 ③当CQ=时, S与C1D1的交点R满足C1R= ④当< CQ< 1时, S为六边形 ⑤当CQ=1时, S的面积为 [解析] 14.过A作AM∥PQ交DD1或A1D1于M. 当0< CQ< 时, M在DD1上, 连MQ, 则截面为AMQP, 故①正确. 当CQ=时, M与D1重合, 截面为AD1QP, 显然为等腰梯形, ②正确. 当CQ=时, M在A1D1上, 且D1M=. 过M作MR∥AP交C1D1于R, 则△MD1R∽△PBA, 从而D1R=, 即C1R=, 故③正确. 当< CQ< 1时, 截面为AMRQP, 为五边形, 即④错误. 当CQ=1时, M为A1D1的中点, 截面AMC1P为菱形, 而AC1=, PM=, 故面积为××=, ⑤正确. 【查看更多】

     

    题目列表(包括答案和解析)

    (本题满分16分)本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分5分．

    如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道，赛道的前一部分为曲线OSM，该曲线段为函数的图像，且图像的最高点为.赛道的后一段为折线段MNP，为保证参赛队员的安全，限定.

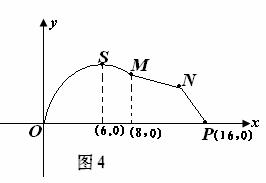
    (1)求实数的值以及M、P两点之间的距离；

    (2)联结MP，设，试求出用的解析式；

    (3)应如何设计，才能使折线段MNP最长？

    查看答案和解析>>

    （本小题满分1 5分）

     如图所示，在棱长为2的正方体中，、分别为、的

    中点．

    （1）求证：//平面；

    （2）求证：；

    （3）求三棱锥的体积．

    查看答案和解析>>

    (本题满分16分)本题共有3个小题，第1小题满分5分，第2小题满分6分，第3小题满分5分．

    如图4,某市拟在长为16km的道路OP的一侧修建一条自行车赛道，赛道的前一部分为曲线OSM，该曲线段为函数的图像，且图像的最高点为.赛道的后一段为折线段MNP，为保证参赛队员的安全，限定.

    (1)求实数的值以及M、P两点之间的距离；

    (2)联结MP，设，试求出用的解析式；

    (3)求函数y的最大值．

    查看答案和解析>>

    （本小题满分1 5分）

     如图所示，在棱长为2的正方体中，、分别为、的

    中点．

    （1）求证：//平面；

    （2）求证：；

    （3）求三棱锥的体积．

    查看答案和解析>>

    11、某校为了了解学生的身体素质情况，对初三（2）班的50名学生进行了立定跳远、铅球、100米三个项目的测试，每个项目满分为10分．如图，是将该学生所得的三项成绩（成绩均为整数）之和进行整理后，分成5组画出的频率分布直方图，已知从左至右前4个小组的频率分别为0.02，0.1，0.12，0.46．
    下列说法：
    （1）学生的成绩≥27分的共有15人；
    （2）学生成绩的众数在第四小组（22.5～26.5）内；
    （3）学生成绩的中位数在第四小组（22.5～26.5）范围内．
    其中正确的说法有（　　）

    查看答案和解析>>


    同步练习册答案