
题目列表(包括答案和解析)






 的方程;
的方程; 为椭圆上任意一点,以
为椭圆上任意一点,以 为圆心,
为圆心, 为半径作圆
为半径作圆 ,当圆
,当圆 与椭圆的右准线
与椭圆的右准线 有公共点时,求△
有公共点时,求△ 面积的最大值
面积的最大值椭圆 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合.
(1)求椭圆 和抛物线
和抛物线 的方程;
的方程;
(2)过点F的直线交抛物线 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值.
(3)直线 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.
 的方程为
的方程为 ,离心率为
,离心率为 ,且短轴一端点和两焦点构成的三角形面积为1,抛物线
,且短轴一端点和两焦点构成的三角形面积为1,抛物线 的方程为
的方程为 ,抛物线的焦点F与椭圆的一个顶点重合.
,抛物线的焦点F与椭圆的一个顶点重合. 和抛物线
和抛物线 的方程;
的方程; 于不同两点A,B,交y轴于点N,已知
于不同两点A,B,交y轴于点N,已知 的值.
的值. 交椭圆
交椭圆 于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足
于不同两点P,Q,P,Q在x轴上的射影分别为P′,Q′,满足 (O为原点),若点S满足
(O为原点),若点S满足 ,判定点S是否在椭圆
,判定点S是否在椭圆 上,并说明理由.
上,并说明理由.设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于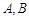 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,求
能否垂直?若能,求 之间满足的关系式;若不能,说明理由;
之间满足的关系式;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求
,求 之间满足的关系式.
之间满足的关系式.
设椭圆的方程为 ,斜率为1的直线不经过原点
,斜率为1的直线不经过原点 ,而且与椭圆相交于
,而且与椭圆相交于 两点,
两点, 为线段
为线段 的中点.
的中点.
(1)问:直线 与
与 能否垂直?若能,
能否垂直?若能, 之间满足什么关系;若不能,说明理由;
之间满足什么关系;若不能,说明理由;
(2)已知 为
为 的中点,且
的中点,且 点在椭圆上.若
点在椭圆上.若 ,求椭圆的离心率.
,求椭圆的离心率.
一、选择题:
1.B 2.A 3.B 4.D 5.D 6.B 7.A
8.B 9.D 10.C 11.A 12.C
二、填空题:
13.1 14..files/image295.gif) 15.20 1 6.32 17.
15.20 1 6.32 17..files/image297.gif)
18、 0 ; 19、.files/image299.gif) ; 20、
; 20、.files/image301.gif) ; 21、 ③ ; 22.①③
; 21、 ③ ; 22.①③
三、解答题:
23解:(Ⅰ)因为.files/image303.gif) ,
,.files/image305.gif) ,所以
,所以
.files/image307.gif)
.files/image309.gif)
因此,当.files/image311.gif) ,即
,即.files/image313.gif) (
(.files/image315.gif) )时,
)时,.files/image197.gif) 取得最大值
取得最大值.files/image318.gif) ;
;
(Ⅱ)由.files/image320.gif) 及
及.files/image322.gif) 得
得.files/image324.gif) ,两边平方得
,两边平方得
.files/image326.gif) ,即
,即.files/image328.gif) .
.
24解:(1)当点.files/image221.gif) 为
为.files/image331.gif) 的中点时,
的中点时,.files/image333.gif) 。
。
理由如下:.files/image335.gif) 点
点.files/image337.gif) 分别为
分别为.files/image223.gif) 、PD的中点,
、PD的中点,
.files/image340.gif)
.files/image342.gif) 。
。
.files/image335.gif)
.files/image345.gif) ,
,.files/image347.gif)
.files/image349.gif)
(2).files/image335.gif)
.files/image213.gif) ,
,.files/image353.gif)
.files/image355.gif)
.files/image357.gif) ,
,.files/image359.gif)
.files/image361.gif) ,
,.files/image363.gif)
.files/image365.gif)
.files/image367.gif)
.files/image369.gif) ,点
,点.files/image217.gif) 是
是.files/image219.gif) 的中点
的中点 .files/image373.gif)
又.files/image375.gif)
.files/image377.gif)
.files/image379.gif)
.files/image381.gif)
25解:(1)依题意知,.files/image383.gif)
∵.files/image385.gif) ,
,.files/image387.gif) .
.
∴所求椭圆.files/image242.gif) 的方程为
的方程为.files/image389.gif) .
.
(2)∵ 点.files/image246.gif)
.files/image248.gif) 关于直线
关于直线.files/image250.gif) 的对称点为
的对称点为.files/image252.gif) ,
,
∴ .files/image392.gif)
解得:.files/image394.gif) ,
,.files/image396.gif) .
.
∴.files/image398.gif) .
.
∵
点.files/image246.gif)
.files/image248.gif) 在椭圆
在椭圆.files/image242.gif) :
:.files/image389.gif) 上,∴
上,∴.files/image400.gif) , 则
, 则.files/image402.gif) .
.
∴.files/image254.gif) 的取值范围为
的取值范围为.files/image405.gif) .
.
26解:(1)当.files/image407.gif) 时,
时,.files/image409.gif) .
.
当.files/image411.gif) 时,
时,.files/image413.gif)
.files/image415.gif)
.files/image417.gif) .
.
∵.files/image419.gif) 不适合上式,
不适合上式,
∴.files/image421.gif)
(2)证明: ∵.files/image423.gif) .
.
当.files/image425.gif) 时,
时,.files/image427.gif)
当.files/image411.gif) 时,
时,.files/image430.gif) ,
①
,
①
.files/image432.gif) .
②
.
②
①-②得:
.files/image434.gif)
.files/image436.gif)
得.files/image438.gif) ,
,
此式当.files/image425.gif) 时也适合.
时也适合.
∴.files/image440.gif) N
N.files/image442.gif) .
.
∵.files/image444.gif) ,
,
∴.files/image446.gif) .
.
当.files/image411.gif) 时,
时,.files/image448.gif) ,
,
∴.files/image450.gif) .
.
∵.files/image452.gif) ,
,
∴.files/image454.gif) .
.
故.files/image456.gif) ,即
,即.files/image458.gif) .
.
综上,.files/image460.gif) .
.
.files/image461.gif) 27解:(I)由图象在
27解:(I)由图象在.files/image283.gif) 处的切线与
处的切线与.files/image285.gif) 轴平行,
轴平行,
知.files/image463.gif) ,∴
,∴.files/image465.gif) ①
①
又.files/image467.gif) ,故
,故.files/image469.gif) ,
,.files/image471.gif) .
.
(II)令.files/image473.gif) ,
,
得.files/image475.gif) 或
或.files/image477.gif)
易证.files/image475.gif) 是
是.files/image480.gif) 的极大值点,
的极大值点,.files/image477.gif) 是极小值点(如图).
是极小值点(如图).
令.files/image483.gif) ,得
,得.files/image475.gif) 或
或.files/image486.gif) .
.
分类:(I)当.files/image488.gif) 时,
时,.files/image490.gif) ,∴
,∴.files/image492.gif) . ②
. ②
由①,②解得.files/image494.gif) ,符合前提
,符合前提.files/image488.gif) .
.
(II)当.files/image496.gif) 时,
时,.files/image498.gif) ,
,
∴.files/image500.gif) . ③
. ③
由①,③得 .files/image502.gif) .
.
记.files/image504.gif) ,
,
∵.files/image506.gif) ,
,
∴.files/image508.gif) 在
在.files/image510.gif) 上是增函数,又
上是增函数,又.files/image496.gif) ,∴
,∴.files/image512.gif) ,
,
∴.files/image514.gif) 在
在.files/image516.gif) 上无实数根.
上无实数根.
综上,.files/image275.gif) 的值为
的值为.files/image494.gif) .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com