
题目列表(包括答案和解析)
本题满分12分)
在直角坐标平面内,已知点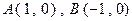 ,动点
,动点 满足
满足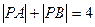 .
.
(1)求动点 的轨迹
的轨迹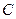 的方程;
的方程;
(2)过点 作直线
作直线 与轨迹
与轨迹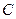 交于
交于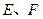 两点,线段
两点,线段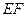 的中点为
的中点为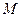 ,轨迹
,轨迹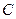 的右端点为点N,求直线MN的斜率
的右端点为点N,求直线MN的斜率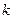 的取值范围.
的取值范围.
(本题满分12分)
如下的三个图中,上面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在下面画出(单位: )
)
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅲ)在所给直观图中连结 ,证明:
,证明: ∥面
∥面

(本题满分12分)
设函数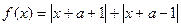 的图象关于y轴对称,函数
的图象关于y轴对称,函数 (b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(b为实数,c为正整数)有两个不同的极值点A、B,且A、B与坐标原点O共线:
(1) 求f(x)的表达式;
(2) 试求b的值;
(3) 若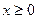 时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
时,函数g(x)的图象恒在函数f(x)图象的下方,求正整数c的值。
本题满分12分)
在直角坐标平面内,已知点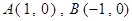 ,动点
,动点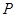 满足
满足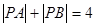 .
.
(1)求动点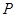 的轨迹
的轨迹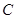 的方程;
的方程;
(2)过点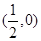 作直线
作直线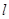 与轨迹
与轨迹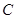 交于
交于 两点,线段
两点,线段 的中点为
的中点为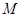 ,轨迹
,轨迹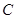 的右端点为点N,求直线MN的斜率
的右端点为点N,求直线MN的斜率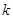 的取值范围.
的取值范围.
一、选择题:(本大题共10小题,每小题5分,共50分)
1 B
B  A 3
A 3 文C(理C) 4
文C(理C) 4 D 5
D 5 文A(理B) 6
文A(理B) 6 文B(理C) 7
文B(理C) 7 文C(理C) 8
文C(理C) 8 文C(理A) 9
文C(理A) 9 文A (理D) 10
文A (理D) 10 文D(理A)
文D(理A)
 三、解答题:(本大题共6个解答题,满分76分,)
三、解答题:(本大题共6个解答题,满分76分,)
线为y轴建立平面直角坐标系如图所示,
则A(-4,0),N(4,0),设P(x,y) 
由|PM|:|PN|= ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:


代入坐标得:

整理得:
即

所以动点P的轨迹是以点


(理)解:(I)当a=1时 



 或
或 或
或

 或
或

(II)原不等式
设 有
有

当且仅当
即 时
时



解得








若由方程组 解得
解得 ,可参考给分
,可参考给分
(理)解:(Ⅰ)设 (a≠0),则
(a≠0),则
 …… ①
…… ①
 …… ②
…… ②
又∵ 有两等根
有两等根
∴ …… ③
…… ③
由①②③得

又∵

∴a<0, 故
∴

(Ⅱ)


∵g(x)无极值
∴方程

得



 或
或 或
或

 或
或

(II)原不等式
设 有
有

当且仅当
即 时
时

(理)解:以AN所在直线为x轴,AN的中垂
线为y轴建立平面直角坐标系如图所示,
则A(-4,0),N(4,0),设P(x,y) 
由|PM|:|PN|= ,|PM|2=|PA|2 ?|MA|2得:
,|PM|2=|PA|2 ?|MA|2得:


代入坐标得:

整理得:
即

所以动点P的轨迹是以点


 …… ①
…… ①
 …… ②
…… ②
又∵ 有两等根
有两等根
∴ …… ③
…… ③
由①②③得

又∵

∴a<0, 故
∴

(Ⅱ)


∵g(x)无极值
∴方程

得

(理)解:(I)设 (1)
(1)
又 故
故 (2)
(2)
由(1),(2)解得

(II)由向量 与向量
与向量 的夹角为
的夹角为 得
得
由 及A+B+C=
及A+B+C= 知A+C=
知A+C=
则






由0<A< 得
得 ,得
,得
故 的取值范围是
的取值范围是

Sn+1=2an+1-3(n+1),两式相减并整理得:an+1=2an+3

所以3+ an+1=2(3+an),又a1=S1=2a1-3,a1=3可知3+
a1=6 ,进而可知an+3
,进而可知an+3
所以 ,故数列{3+an}是首相为6,公比为2的等比数列,
,故数列{3+an}是首相为6,公比为2的等比数列,
所以3+an=6 ,即an=3(
,即an=3( )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com