练习册

  • 练习册
  • 试题
    三.解答题 12.某厂工人在一年里如果有1个季度完成生产任务,则可得奖金300元;如果有2个季度完成生产任务,则可得奖金750元;如果有3个季度完成生产任务,则可得奖金1260元;如果有4个季度完成生产任务,则可得奖金1800元;如果四个季度都未完成任务,则没有奖金.假设某工人每季度完成任务与否是等可能的,求他在一年里所得奖金的分布列. 解:设该工人在一年里所得奖金为X, 则X是一个离散型随机变量. 由于该工人每季度完成任务与否是等可能的,所以他每季度完成任务的概率等于,所以 P(X=0)=, P(X=300)=, P(X=750)=, P(X=1260)=, P(X=1800)=. 故X的分布列为 X 0 300 750 1260 1800 P 13.现有4个人去参加某娱乐活动,该活动有甲.乙两个游戏可供参加者选择.为增加趣味性,约定:每个人通过掷一枚质地均匀的骰子决定自己去参加哪个游戏,掷出点数为1或2的人去参加甲游戏,掷出点数大于2的人去参加乙游戏. (1)求这4个人中恰有2人去参加甲游戏的概率; (2)求这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率; (3)用X,Y分别表示这4个人中去参加甲.乙游戏的人数,记ξ=|X-Y|,求随机变量ξ的分布列与数学期望E(ξ). 解:依题意,这4个人中,每个人去参加甲游戏的概率为,去参加乙游戏的概率为. 设“这4个人中恰有i人去参加甲游戏 为事件Ai(i=0,1,2,3,4), 则P(Ai)=. (1)这4个人中恰有2人去参加甲游戏的概率P(A2)=. (2)设“这4个人中去参加甲游戏的人数大于去参加乙游戏的人数 为事件B,则B=A3∪A4.由于A3与A4互斥,故 P(B)=P(A3)+P(A4) =. 所以,这4个人中去参加甲游戏的人数大于去参加乙游戏的人数的概率为. (3)ξ的所有可能取值为0,2,4. 由于A1与A3互斥,A0与A4互斥,故 P(ξ=0)=P(A2)=, P(ξ=2)=P(A1)+P(A3)=, P(ξ=4)=P(A0)+P(A4)=. 所以ξ的分布列是 ξ 0 2 4 P 随机变量ξ的数学期望E(ξ)=0×+2×+4×. 14.某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为,第二.第三门课程取得优秀成绩的概率分别为p,q(p>q),且不同课程是否取得优秀成绩相互独立.记ξ为该生取得优秀成绩的课程数,其分布列为 ξ 0 1 2 3 P a b (1)求该生至少有1门课程取得优秀成绩的概率; (2)求p,q的值; (3)求数学期望E(ξ). 解:事件Ai表示“该生第i门课程取得优秀成绩 ,i=1,2,3. 由题意知P(A1)=,P(A2)=p,P(A3)=q. (1)由于事件“该生至少有1门课程取得优秀成绩 与事件“ξ=0 是对立的,所以该生至少有1门课程取得优秀成绩的概率是 1-P(ξ=0)=1-. (2)由题意知 P(ξ=0)=P()=(1-p)(1-q)=, P(ξ=3)=P(A1A2A3)=pq=. 整理得pq=,p+q=1. 由p>q,可得p=,q=. (3)由题意知 a=P(ξ=1)=P(A1)+P( A2)+P( A3)=(1-p)(1-q)+p(1-q)+(1-p)q=, b=P(ξ=2)=1-P(ξ=0)-P(ξ=1)-P(ξ=3)=. 所以E(ξ)=0×P(ξ=0)+1×P(ξ=1)+2×P(ξ=2)+3×P(ξ=3)=. 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)

    某厂工人在2010年里,如果有1个季度完成生产任务，则得奖金300元；如果有2个季度完成生产任务，则可得奖金750元；如果有3个季度完成生产任务，则可得奖金1260元；如果有4个季度完成生产任务，可得奖金1800元；如果工人四个季度都未完成任务，则没有奖金，假设某工人每季度完成任务与否是等可能的，求他在2010年一年里所得奖金的分布列及其数学期望。

     

    查看答案和解析>>

     

    三、解答题(共75分)

    【题文】

     (12分) 在

        (I)求AB的值；

        (Ⅱ)求的值。

     

     

    查看答案和解析>>

    附加题(本题满分10分)

        某厂生产某种零件,每个零件的成本为元,出厂单价定为元,该厂为鼓励销售部门订购,决定当一次订购量超过个时,每多订购一个，订购全部零件的出厂单价就降元,但实际出厂单价不能低于元．

    （Ⅰ)当一次订购量为多少时，零件的实际出厂单价恰降为元？

    （Ⅱ)当一次订购量为个，零件的实际出厂单价为元，写出函数的表达式.

    （Ⅲ)当销售商一次订购个零件时,该厂获得的利润是多少元?如果订购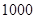个,利润是多少元?

     

    查看答案和解析>>

    某厂工人在2008年里有1个季度完成生产任务，则得奖金300元；如果有2个季度完成生产任务，则可得奖金750元；如果有3个季度完成生产任务，则可得奖金1260元；如果有4个季度完成生产任务，可得奖金1800元；如果工人四个季度都未完成任务，则没有奖金，假设某工人每季度完成任务与否是等可能的，求他在2008年一年里所得奖金的分布列．

    查看答案和解析>>

    某厂工人在2012年里有1个季度完成生产任务，则得奖金300元；如果有2个季度完成生产任务，则可得奖金750元；如果有3个季度完成生产任务，则可得奖金1260元；如果有4个季度完成生产任务，可得奖金1800元；如果工人四个季度都未完成任务，则没有奖金，假设某工人每季度完成任务与否是等可能的，求他在2012年一年里所得奖金的分布列．）

    查看答案和解析>>


    同步练习册答案