练习册

  • 练习册
  • 试题
    21． 证明:(1)连接. ∵, ∴. 又∵ ∴ 又∵. ∴ --------1分 ∴OC∥DB. ∵CE⊥DB. ∴. 又∵为⊙的半径. ∴为⊙O的切线． ---------------------2分 (2)连结. 在Rt△BEF中.∠BEF=90°, BF=5, . ∴. --------------------------3分 ∵OC∥BE, ∴∽. ∴ 设⊙的半径为r, ∴ ∴. --------------------------4分 ∵AB为⊙O直径. ∴. ∴. ∵, ∴. ∴ ∴ ∴．--------------------------5分 【查看更多】

     

    题目列表(包括答案和解析)

    已知AB是⊙O的直径，C是⊙O上一点，连接AC，过点C作CD⊥AB于点D．

    (1)当点E为DB上任意一点(点D、B除外)时，连接CE并延长交⊙O于点F，AF与CD的延长线交于点G(如图①)．求证：AC2＝AG·AF．

    (2)李明证明(1)的结论后，又作了以下探究：当点E为AD上任意一点(点A、D除外)时，连接CE并延长交⊙O于点F，连接AF并延长与CD的延长线在圆外交于点G，CG与⊙O相交于点H(如图②)．连接FH后，他惊奇的发现∠GFH＝∠AFC．根据这一条件，可证GF·GA＝GH·GC．请你帮李明给出证明．

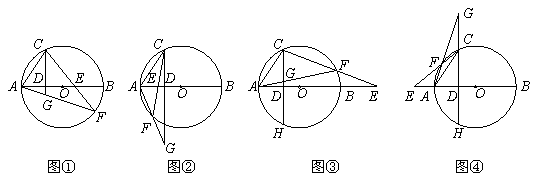    (3)当点E为AB的延长线上或反向延长线上任意一点(点A、B除外)时，如图③、④所示，还有许多结论成立．请你根据图③或图④再写出两个类似问题(1)、(2)的结论(两角、两弧、两线段相等或不相等的关系除外)(不要求证明)．

    查看答案和解析>>

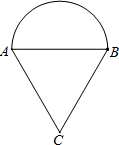    如图，已知等边△ABC，以AB为直径向外做半圆．
    （1）请用直尺和圆规作该半圆的三等点D、E；（要保留作图痕迹，不写作法与证明）
    （2）连接CD交AB于F，求
    DFCF
    的值．

    查看答案和解析>>

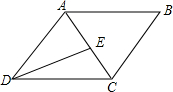    如图，已知E是平行四边形ABCD对角线AC上的点，连接DE．
    （1）过点B在平行四边形内部作射线BF交AC于点F，且使∠CBF=∠ADE（要求：用尺规作图，保留作图痕迹，不写作法与证明）
    （2）连接BE，DF，判断四边形BFDE的形状并证明．

    查看答案和解析>>

    21、已知在四边形ABCD中，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形．
    请你思考下面的证法对吗？如果不对，错在何处并请给出另一种证明过程．
    证明：如图，连接BD，则∠1+∠3=180°-∠A，∠2+∠4=180°-∠C．
    ∵∠A=∠C，∴∠1+∠3=∠2+∠4．
    ∵∠B=∠D，∴∠1=∠4，∠2=∠3．
    ∴AB∥CD，AD∥BC．
    ∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形）．

    查看答案和解析>>

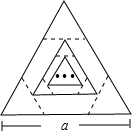    边长为a的等边三角形，记为第1个等边三角形．取其各边的三等分点，顺次连接得到一个正六边形，记为第1个正六边形．取这个正六边形不相邻的三边中点顺次连接，又得到一个等边三角形，记为第2个等边三角形．取其各边的三等分点，顺次连接又得到一个正六边形，记为第2个正六边形（如图）…，按此方式依次操作．则第6个正六边形的边长是
    1
    96
    a
    1
    96
    a
    ．

    查看答案和解析>>


    同步练习册答案