我们知道Rt△ABC中，∠A＝时，就有BC²＝AC²＋AB²，反过来在△ABC中，若有AC²＋AB²＝BC²，是否存在∠A＝这样的结论呢？下面就这个问题我们进行探究．

已知△ABC中，AC²＋AB²＝BC²．

求证：∠A＝．

证明：作，使＝，

＝AB，＝AC，

∴＝＋．

∴＝AB²＋AC²．又∵BC²＝AB²＋AC²，

∴_____________

在△ABC和中，

∴_____________

∴_____________

(1)补充上述证明过程空缺的部分；

(2)上面已证的命题就是勾股定理的逆定理，可以直接运用上述的结论解决下面的问题：

已知正方形ABCD，AB＝a，点E为AB的中点，点F在AD边上，且AF＝AD，用两种不同的方法证明：EF⊥CE．

如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.

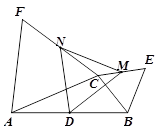
1.求证：△DMN是等边三角形；

2.连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.

同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：

小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.

如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.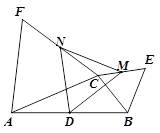

【小题1】求证：△DMN是等边三角形；
【小题2】连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.
同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：
小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.

如图，D是△ABC中AB边的中点，△BCE和△ACF都是等边三角形， M、N分别是CE、CF的中点.

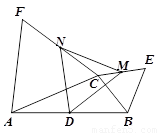
1.求证：△DMN是等边三角形；

2.连接EF，Q是EF中点，CP⊥EF于点P. 求证：DP＝DQ.

同学们，如果你觉得解决本题有困难，可以阅读下面两位同学的解题思路作为参考：

小聪同学发现此题条件中有较多的中点，因此考虑构造三角形的中位线，添加出了一些辅助线；小慧同学想到要证明线段相等，可通过证明三角形全等，如何构造出相应的三角形呢？她考虑将△NCM绕顶点旋转到要证的对应线段的位置，由此猜想到了所需构造的三角形的位置.