
题目列表(包括答案和解析)
(本题满分10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
(本题满分10分)在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
(本题满分9分)
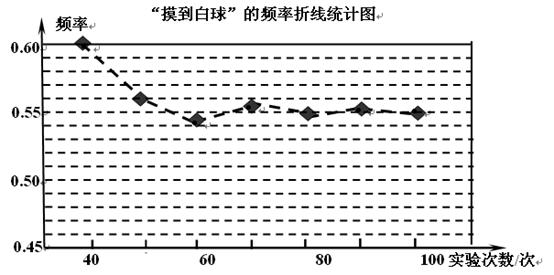
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:
(1)请估计:当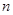 很大时,摸到白球的频率将会接近 (精确到0.01);
很大时,摸到白球的频率将会接近 (精确到0.01);
(2)假如你摸一次,你摸到黑球的概率P(黑球)= ;
(3)试估算盒子里白、黑两种颜色的球各有多少个?
(4)在(2)条件下如果要使摸到白球的概率为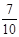 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
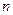 很大时,摸到白球的频率将会接近 (精确到0.01);
很大时,摸到白球的频率将会接近 (精确到0.01);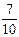 ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com