设a为实数，记函数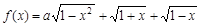的最大值为．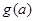

（1）设t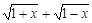＝，求t的取值范围，并把f(x)表示为t的函数m(t) ；

（2）求 ；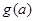

（3）试求满足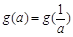的所有实数a．

设a为实数，记函数的最大值为g（a）.

   （1）设t＝，求t的取值范围，并把f（x）表示为t的函数m（t）；

   （2）求g（a）；

   （3）试求满足的所有实数a．

（本小题满分14分）

       设a为实数，记函数的最大值为g（a）.

   （1）设t＝，求t的取值范围，并把f（x）表示为t的函数m（t）；

   （2）求g（a）；

   （2）试求满足的所有实数a．

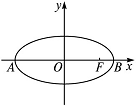
在平面直角坐标系xOy中，如图，已知椭圆＝1的左、右顶点为A、B，右焦点为F.设过点T(t，m)的直线TA，TB与此椭圆分别交于点M(x₁，y₁)、N(x₂，y₂)，其中m＞0，y₁＞0，y₂＜0.

(1)设动点P满足PF²－PB²＝4，求点P的轨迹；

(2)设x₁＝2，x₂＝，求点T的坐标；

(3)设t＝9，求证：直线MN必过x轴上的一定点(其坐标与m无关)．

（本题满分13分）已知函数f（x）＝2x²－2ax＋b，f（－1）＝－8．对x∈R，都有f（x）≥f（－1）成立；记集合A＝{ x | f（x）＞0}，B＝{ x | | x－t |≤1 }．（1） 当t＝1时，求（_RA）∪B；（2） 设命题P：A∩B≠，若┐P为真命题，求实数t的取值范围．