
题目列表(包括答案和解析)
(1) (2)
图13
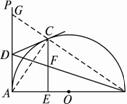
(1)当点C为![]() 的中点时(如图13(1)),求证:CF =EF;
的中点时(如图13(1)),求证:CF =EF;
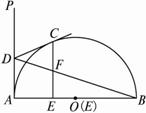
(2)当点C不是![]() 的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
的中点时(如图13(2)),试判断CF与EF的相等关系是否保持不变,并证明你的结论.
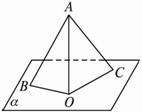
 (2012•成都模拟)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点.
(2012•成都模拟)如图,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE=2,F为CD中点. (2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点
(2010•天津模拟)如图,PA⊥平面ABCD,ABCD是矩形,PA=AB=1,PD与平面ABCD所成的角是30°,点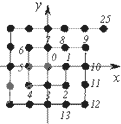 如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签;原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2013×2014对应的格点的坐标为
如图,将平面直角坐标系中的格点(横、纵坐标均为整数的点)按如下规则标上数字标签;原点(0,0)处标0,点(1,0)处标1,点(1,-1)处标2,点(0,-1)处标3,点(-1,-1)处标4,点(-1,0)处标5,…,依此类推,则标签2013×2014对应的格点的坐标为湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com