
题目列表(包括答案和解析)
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.


图1 图2
(1)求证:A1C⊥平面BCDE;
(2)过点E作截面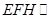 平面
平面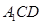 ,分别交CB于F,
,分别交CB于F,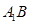 于H,求截面
于H,求截面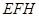 的面积;
的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成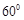 的角?说明理由.
的角?说明理由.
已知函数![]() 满足以下三个条件:(1)在
满足以下三个条件:(1)在![]() 上是增函数;(2)以
上是增函数;(2)以![]() 为最小正周期;(3)是偶函数,试写出一满足以上性质的一个函数解析式 .
为最小正周期;(3)是偶函数,试写出一满足以上性质的一个函数解析式 .
如图,四棱柱 中,
中,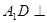 平面
平面 ,底面
,底面 是边长为
是边长为 的正方形,侧棱
的正方形,侧棱 .
.

(1)求三棱锥 的体积;
的体积;
(2)求直线 与平面
与平面 所成角的正弦值;
所成角的正弦值;
(3)若棱 上存在一点
上存在一点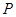 ,使得
,使得 ,当二面角
,当二面角 的大小为
的大小为 时,求实数
时,求实数 的值.
的值.
【解析】(1)在 中,
中,
 .
(3’)
.
(3’)
(2)以点D为坐标原点,建立如图所示的空间直角坐标系 ,则
,则
 (4’)
(4’)
 ,设平面
,设平面 的法向量为
的法向量为 ,
,
由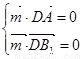 得
得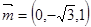 ,
(5’)
,
(5’)
则 ,
,
 . (7’)
. (7’)
(3)
设平面 的法向量为
的法向量为 ,由
,由 得
得 ,
(10’)
,
(10’)

| OA |
| OB |
| AC |
A、{
| ||||||||
| B、{-1} | ||||||||
| C、? | ||||||||
| D、{-1,0} |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com