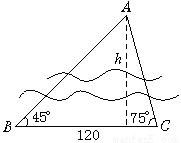
欲测河的宽度，在一岸边选定A、B两点，望对岸的标记物C，测得∠CAB＝45°，∠CBA＝75°，AB＝120 m，求河宽.（精确到0.01 m）

解析　“指数函数y＝a^x是增函数”是本推理的大前提，它是错误的，因为实数a的取值范围没有确定，所以导致结论是错误的．

答案　A

（08年潍坊市七模） （12分）在Rt△ABC中，∠CAB＝90°，AB＝2，AC＝，一曲线E过C点，动点P在曲线E上运动，且保持的值不变．

　　（1）建立适当的坐标系，求曲线E的方程；

　　（2）直线l：与曲线E交于M，N两点，求四边形MANB的面积的最大值．

　D

[解析]　⊙C₁：(x＋a)²＋y²＝4的圆心C₁(－a,0)，半径r₁＝2，⊙C₂：x²＋(y－b)²＝1的圆心C₂(0，b)，半径r₂＝1，

∵⊙C₁与⊙C₂外切，∴|C₁C₂|＝r₁＋r₂，

∴a²＋b²＝9，

∵(a＋b)²＝a²＋b²＋2ab≤2(a²＋b²)＝18，

∴a＋b≤3，等号在a＝b＝时成立．

已知定义在R上的奇函数　f(x)有最小正周期2，且当x∈(0,1)时，　f(x)＝.

(1)  求　f(x)在[－1,1]上的解析式；

(2)  证明：　f(x)在(0,1)上是减函数．