(2010•高要市二模)为了让学生了解环保知识,增强环保意识,某中学举行了一次大规模的“环保知识竞赛”,初中三个年级共有900名学生参加了初赛,为了解本次初赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.
频数分布表
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | | |
| 合计 | | |
(一)请你根据下面尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
(1)填充频率分布表中的空格:
(2)补全频率分布直方图:
(3)在该问题中的样本容量是多少?答:______.
(4)全体参赛学生中,竞赛成绩落在哪组范围内的人数最多?(不要求说明理由)答:______.
(5)若成绩在80分以上(不含80分)为优良,则该成绩优良的约为多少人?答:______.
(二)初中三个年级根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分为100分)如下表所示:
| | 决赛成绩(单位:分) |
| 初一年级 | 80 | 86 | 88 | 80 | 88 | 99 | 80 | 74 | 91 | 89 |
| 初二年级 | 85 | 85 | 87 | 97 | 85 | 76 | 88 | 77 | 87 | 88 |
| 初三年级 | 82 | 80 | 78 | 78 | 81 | 96 | 97 | 88 | 89 | 86 |
(6)请你填写下表:
| | 平均数 | 众数 | 中位数 |
| 初一年级 | 85.5 | 80 | |
| 初二年级 | 85.5 | | 86 |
| 初三年级 | | | 84 |
(7)请从以下两个不同的角度对三个年级的决赛成绩进行分析:
<1>从平均数和众数相结合看(分析哪个年级成绩好些).
<2>从平均数和中位数相结合看(分析哪个年级成绩好些).
(8)如果在每个年级参加决赛的选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些?并说明理由.


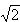 ,若
,若 ABC固定不动,
ABC固定不动, AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n
AFG绕点A旋转,AF、AG与边BC的交点分别为D、E(点D不与点B重合,点E不与点C重合),设BE=m,CD=n  ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系
ABC的斜边BC所在的直线为x轴,BC边上的高所在的直线为y轴,建立平面直角坐标系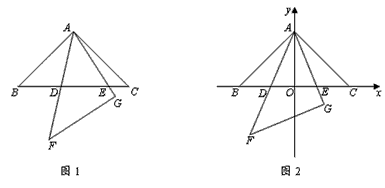





 在一场篮球比赛中,一球星将球出手时,球离地面
在一场篮球比赛中,一球星将球出手时,球离地面