
题目列表(包括答案和解析)
(本小题满分12分)
某校高三(1)班共有 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在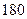 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [180 , 210) |  |  |
| [210 , 240) |  |  |
| [240 , 270) |  |  |
| [270 , 300) |  |  |
| [300 , 330) |  |  |
 ,
, 的值;
的值; 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生? 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.(本小题满分12分)
某校高三(1)班共有![]() 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在![]() 分钟到
分钟到![]() 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分![]() 个组统计得到如下频率分布表:
个组统计得到如下频率分布表:
| 分组 | 频数 | 频率 |
| [180 , 210) |
|
|
| [210 , 240) |
|
|
| [240 , 270) |
|
|
| [270 , 300) |
|
|
| [300 , 330) |
|
|
(1)求分布表中![]() ,
,![]() 的值;
的值;
(2)某兴趣小组为研究每天自主学习的时间与学习成绩的相关性,需要在这![]() 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取![]() 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生?
(3)已知第一组的学生中男、女生均为![]() 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
 名学生,他们每天自主学习的时间全部在
名学生,他们每天自主学习的时间全部在 分钟到
分钟到 分钟之间,按他们学习时间的长短分
分钟之间,按他们学习时间的长短分 个组统计得到如下频率分布表:
个组统计得到如下频率分布表: | 分组 | 频数 | 频率 |
| [180 , 210) |  | 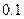 |
| [210 , 240) |  |  |
| [240 , 270) |  |  |
| [270 , 300) |  |  |
| [300 , 330) |  |  |
 ,
, 的值;
的值; 名学生中按时间用分层抽样的方法抽取
名学生中按时间用分层抽样的方法抽取 名学生进行研究,问应抽取多少名第一组的学生?
名学生进行研究,问应抽取多少名第一组的学生? 人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.
人.在(2)的条件下抽取第一组的学生,求既有男生又有女生被抽中的概率.(本小题满分12分)某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为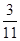 .
.
|
|
优秀 |
非优秀 |
合计 |
|
甲班 |
10 |
|
|
|
乙班 |
|
30 |
|
|
合计 |
|
|
110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
附: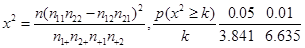 )
)
(本小题满分12分)
某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区.
(Ⅰ)求互换后两校派往两地区教师人数不变的概率;
(Ⅱ)求互换后A校教师派往甲地人数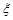 的分布列和数学期望.
的分布列和数学期望.
一、1.B 2.B 3.D 4.B 5.D 6.A 7.B 8.C 9.B 10.B 11.B 12.D
二、13. 14.32 15.162 16.3
三、17.解:(1)
(2)
,
18.解:(1)设5次实验中只成功一次为事件A,一次都不成功为事件B,
则P(5次实验至少2次成功)=1-P(A)-P(B)=1-
(法2:所求概率为)
(2)ξ的可能取值为2、3、4、5
又
19.解法1:(1)取CD的中点E,连结PE、EM、EA
∵△PCD为正三角形 ∴PE⊥CD,PE=PDsin∠PDE=2sin60°=
∵平面PCD⊥平面ABCD ∴PE⊥平面ABCD
∵四边形ABCD是矩形 ∴△ADE、△ECM、△ABM均为直角三角形
由勾股定理可求得EM=,AM=,AE=3 ∴EM2+AM2=AE2
∴∠AME=90° ∴AM⊥PM
(2)由(1)可知EM⊥AM,PM⊥AM ∴∠PME是二面角P―AM―D的平面角
∴tan∠PME= ∴∠PMA=45° ∴二面角P―AM―D为45°
(3)设D点到平面PAM的距离为d,连结DM,则
在Rt△PEM中,由勾股定理可求得PM=,,
解法2:(1)以D点为原点,
分别以直线DA、DC
为x轴、y轴,建立
如图所示的空间直角
坐标系D―xyz,
依题意,可得D(0,0,0),P(0,1,),C(0,2,0),A(2,0,0),
M(,2,0),
即,∴AM⊥PM.
(2)设平面PAM,则
取y=1,得 显然平面ABCD
.
结合图形可知,二面角P―AM―D为45°;
(3)设点D到平面PAM的距离为d,由(2)可知)与平面PAM垂直,
则
即点D到平面PAM的距离为
20.解:(1)
①当时 由
解得:定义域为(0,+∞)
∴函数的单调递增区间为(
由可知的单调递增区间为
②当时 同理可得:函数的单调递增区间为
函数的单调递减区间为
(2)当时,
令
当上单调递增
当上单调递减
又在[1,3]上连续 为函数的极大值.
又
是函数在[1,3]上的最小值,
为在[1,3]的最大值.
21.解:(1)在直线
∵P1为直线l与y轴的交点,∴P1(0,1) ,
又数列的公差为1
(2)
(3)
是以2为公比,4为首项的等比数列,
22.解:(1)直线l过点(3,)且方向向量为)
∴l方程为 化简为:
∵直线和椭圆交于两点和x轴交于M(1,0)
又
即
(2) ∴椭圆C方程为
由
∴椭圆C方程为:
(3)将中得 ①
由韦达定理知:
由②2/③知:………④
对方程①求判别式,且由 即
化简为:………………⑤
由④式代入⑤式可知:,求得,
又椭圆的焦点在x轴上,则,
由④知:,结合,求得
因此所求椭圆长轴长2a范围为(2,).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com