
题目列表(包括答案和解析)
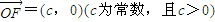 ,
,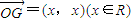 ,|
,| 的最小值为1,
的最小值为1, )(a为常数,且a>c,t∈R).动点P同时满足下列三个条件:
)(a为常数,且a>c,t∈R).动点P同时满足下列三个条件: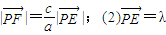 •
•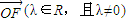 ;
;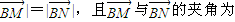 60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.| OF |
| OG |
| FG |
| OE |
| a2 |
| C |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
| BM |
| BN |
| BM |
| BN |
 的距离与它到点
的距离与它到点 的距离之比是
的距离之比是 .
.  的直线l,l与曲线C相交于M、N两点,使
的直线l,l与曲线C相交于M、N两点,使 ,且
,且 与
与 夹角为60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.
夹角为60°?若存在,求出k值,并写出直线l的方程;若不存在,请说明理由.3
| ||
| 2 |
| 2 |
| ||
| 2 |
| m |
| BM |
| BN |
| BM |
| BN |
| OF |
| OG |
| FG |
| OE |
| a2 |
| c |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
| m |
| BM |
| BN |
| BM |
| BN |
一.选择题(本大题共8小题,每小题5分,共40分)
(1)A (2)D (3) B (4) D
(5)D (6)A (7) B (8) C
二.填空题(本大题共6小题,每小题5分,共30分)
(9) (1,-1) (10)试卷.files\image133.gif) ,
,试卷.files\image135.gif) (11) 2 (12)R ,
(11) 2 (12)R ,试卷.files\image137.gif) R
R
(13)
2
(14) 试卷.files\image139.gif)
三.解答题(本大题共6小题,共80分)
15. 解:(Ⅰ)试卷.files\image141.gif) . ………………………………3分
. ………………………………3分
又试卷.files\image143.gif) ,cosC=
,cosC=试卷.files\image145.gif) >0,
>0,
故在试卷.files\image096.gif) 中,
中,试卷.files\image147.gif) 、
、试卷.files\image149.gif) 是锐角. ∴
是锐角. ∴试卷.files\image151.gif) ,
,试卷.files\image153.gif) .
.
∴试卷.files\image155.gif) . ……………………7分
. ……………………7分
(Ⅱ) 试卷.files\image157.gif) .
……………………10分
.
……………………10分
由正弦定理 试卷.files\image159.gif) . 解得
. 解得试卷.files\image161.gif) ,c=6.
,c=6.
∴试卷.files\image163.gif) . ∴
. ∴试卷.files\image165.gif) ,即AC=5 . ……………………13分
,即AC=5 . ……………………13分
16. 解:(I)依条件得试卷.files\image167.gif) , ……………………2分
, ……………………2分
解得试卷.files\image169.gif) .
…………………………………………4分
.
…………………………………………4分
所以an=3+(n-1)=n+2. …………………………………………6分
(II)Pn=试卷.files\image171.gif) , b6=2×26-1=64,
, b6=2×26-1=64,
由试卷.files\image173.gif) >64得n2+5n-128>0.
………………………………9分
>64得n2+5n-128>0.
………………………………9分
所以n(n+5)>128.
因为n是正整数,且n=9时,n(n+5)=126,且n(n+5)是递增的,
所以当n≥10时,n(n+5)>128.
即n≥10时,Pn> b6. …………………………………………………13分
17. 解:(I)甲答对试题数试卷.files\image106.gif) 的可能取值为
的可能取值为试卷.files\image176.gif) 0、1、2、3.
0、1、2、3.
∵试卷.files\image178.gif) ,
,试卷.files\image180.gif) ,
,
试卷.files\image182.gif) ,
,试卷.files\image184.gif) ,
…………………………4分
,
…………………………4分
∴ 甲答对试题数试卷.files\image106.gif) 的概率分布如下:
的概率分布如下:
试卷.files\image106.gif)
0
1
2
3
P
试卷.files\image188.gif)
试卷.files\image190.gif)
试卷.files\image192.gif)
试卷.files\image194.gif)
故甲答对试题数试卷.files\image106.gif) 的数学期望为
的数学期望为
试卷.files\image197.gif)
试卷.files\image199.gif) .
…………………………7分
.
…………………………7分
(II)设甲、乙两人通过测试的事件分别为A、B,则
试卷.files\image201.gif) ,
,
试卷.files\image203.gif) .
…………………………………………9分
.
…………………………………………9分
试卷.files\image205.gif) 、B相互独立,
、B相互独立,
∵甲、乙两人都未通过测试的概率为
试卷.files\image207.gif) . ……………………………11分
. ……………………………11分
∴甲、乙两人至少有一个通过测试的概率为
试卷.files\image209.gif) .
………………………………………13分
.
………………………………………13分
18. (Ⅰ)解:∵正三棱柱中AC∥A
∴∠CAD是异面直线AD与A
连结CD,易知AD=CD=试卷.files\image211.gif) a,AC= a,
a,AC= a,
在△ACD中易求出cos∠CAD=试卷.files\image213.gif) .
.
因此异面直线AD与A试卷.files\image213.gif) . …………………………4分
. …………………………4分
(Ⅱ)证明:
∵D是B1B的中点,
∴△C1B1D≌△ABD.
∴AD= C1D.
试卷.files\image214.gif) 于是△ADC1是等腰三角形.
于是△ADC1是等腰三角形.
∵E是AC1的中点,
∴DE⊥AC1. ……………………6分
设AC的中点为G,
∴EG∥C试卷.files\image216.gif) C
C
∴四边形EGBD是平行四边形.
∴ED∥GB.
∵G是AC的中点,且AB=BC,
∴GB⊥AC.
∴ED⊥AC.
∵AC∩AC1=A,
∴ED⊥平面ACC
(或证ED∥GB,GB⊥平面ACC
(Ⅲ)解:∵C1D,CB共面,
故C1D,CB必相交,设交点为F,连结AF.
∴平面ADC1与平面ABC所成二面角是C-AF-C1. ………………………………10分
∵DB=试卷.files\image216.gif) C
C
∴B是CF的中点.
∴AC=CB=BF= a.
在△ACF中,由余弦定理可求出AF=试卷.files\image218.gif) a.
a.
∴易判断出△ACF是直角三角形,即AC⊥AF.
∵C
∴AC1⊥AF.
∴∠C
∵tan∠C试卷.files\image220.gif) =2,
=2,
∴平面ADC1与平面ABC所成二面角的大小是arctan2(或arccos试卷.files\image222.gif) ). …………13分
). …………13分
19. 解:(Ⅰ)∵试卷.files\image224.gif) ,
,
∴试卷.files\image226.gif) .
……………………………………3分
.
……………………………………3分
令试卷.files\image228.gif) 得,
得,试卷.files\image230.gif) =0
=0试卷.files\image232.gif) .
.
试卷.files\image234.gif) ,
,
∴试卷.files\image236.gif) 方程有两个不同的实根
方程有两个不同的实根试卷.files\image238.gif) 、
、试卷.files\image240.gif) .
.
令试卷.files\image242.gif) ,由
,由试卷.files\image244.gif) 可知:
可知:
当试卷.files\image246.gif) 时,
时,试卷.files\image248.gif) ;
;
当试卷.files\image250.gif) ;
;
当试卷.files\image252.gif) ;
;
∴试卷.files\image238.gif) 是极大值点,
是极大值点,试卷.files\image240.gif) 是极小值点. ……………………………………7分
是极小值点. ……………………………………7分
(Ⅱ)试卷.files\image254.gif) ,
,
所以得不等式试卷.files\image256.gif) .
.
即试卷.files\image258.gif) . ………10分
. ………10分
又由(Ⅰ)知试卷.files\image260.gif) ,
,
代入前面的不等式,两边除以(1+a),
并化简得试卷.files\image262.gif) ,解之得:
,解之得:试卷.files\image264.gif) ,或
,或试卷.files\image266.gif) (舍去).
(舍去).
所以当试卷.files\image264.gif) 时,不等式
时,不等式试卷.files\image117.gif) 成立. …………………………14分
成立. …………………………14分
20. 解:(Ⅰ)∵|试卷.files\image270.gif)
∴试卷.files\image272.gif) .
…………………………………………………2分
.
…………………………………………………2分
由试卷.files\image274.gif) ,
, 试卷.files\image276.gif) .
.
由(1)、(2)可知点P到直线x=试卷.files\image278.gif) ,
,
再由椭圆的第二定义可知,点P的轨迹C是椭圆. …………………………4分
设椭圆C的方程为:试卷.files\image280.gif) ,
,试卷.files\image282.gif)
由(3)可知b =1,∴a2=b2+c2=1+2=3.
∴椭圆C的方程为: 试卷.files\image284.gif) .
…………………………………5分
.
…………………………………5分
(Ⅱ)假设存在符合条件的直线l,并设l的方程为:y=kx+m,M(x1,y1)、N(x2,y2),
试卷.files\image285.gif)
试卷.files\image287.gif) .
.
则x1+x2= -试卷.files\image289.gif) . ………………7分
. ………………7分
Δ=36 k
设线段MN的中点G(x0,y0),
x0=试卷.files\image291.gif) ,
,
线段MN的垂直平分线的方程为:y -试卷.files\image293.gif) .
.
∵|试卷.files\image295.gif) , ∴线段MN的垂直平分线过B(0,-1)点.
, ∴线段MN的垂直平分线过B(0,-1)点.
∴-1-试卷.files\image297.gif) . ∴m=
. ∴m=试卷.files\image299.gif) . ② ………9分
. ② ………9分
②代入①,得3k2 -(试卷.files\image301.gif) . ③
. ③
∵|试卷.files\image303.gif) 的夹角为60°,∴△BMN为等边三角形.
的夹角为60°,∴△BMN为等边三角形.
∴点B到直线MN的距离d=试卷.files\image305.gif) .
…………………………10分
.
…………………………10分
∵试卷.files\image307.gif) ,
,
又∵|MN|=试卷.files\image309.gif)
=试卷.files\image311.gif)
=试卷.files\image313.gif) ,
,
∴试卷.files\image315.gif) . …………………………13分
. …………………………13分
解得k2=试卷.files\image317.gif) ,满足③式. 代入②,得m=
,满足③式. 代入②,得m=试卷.files\image319.gif) .
.
直线l的方程为:y=试卷.files\image321.gif) . ……………………………………………14分
. ……………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com