题目列表(包括答案和解析)
|
| A、（0，1） |
| B、（-1，0） |
| C、（1，+∞） |
| D、（-∞，-1） |
|
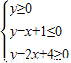，若z=y-ax取得最大值时的唯一最优解是（3，2），则实数a的值范围为（ ）
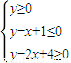，若z=y-ax取得最大值时的唯一最优解是（3，2），则实数a的值范围为（ ）
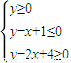，若z=y-ax取得最大值时的唯一最优解是（3，2），则实数a的值范围为（ ）一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
C
B
B
C
B
D
C
B
C
D
C
二、填空题
13.
14.
15.1<m<2 16.2x+6
三、解答题
17.(1)将正弦定量代入条件得：
…………2分
即2sinAcosB+sinCcosB+sinBcosC=0
2sinAcosB+sin(B+C)=0
由B+C=π-A，得2sinAcosB+sinA=0 …………4分
又sinA>0,∴cosB=-
,又0<B<π，∴B=
…………6分
(2)由余弦定理有：b2=a2+c2-2accosB=a2+c2+ac=(a+c)2-ac将b=
,a+c=4代入得ac=3
…………10分
∴S△ABC=
…………12分
18.(1)由Sn=
(an+1)2,且an>0,得a1=S1=(a1+1)2,解得a1=1n≥2时，an=Sn-Sn-1=(an+1)2-(an-1+1)2
(an-1)2-(an-1+1)2=0, (an+an-1)(an-an-1-2)=0
∴an-an-1-2=0, 即an-an-1=2, ∴{an}是公差为2的等数列
∴an=2n-1 …………6分
(2)Cn=
Tn=
∴
∴Tn=1+1
…………12分
19.(1)20个数中有3的倍数6个，除以3余1的7个，余2的7个 …………2分
P1=
…………6分
(2)20个奇数有10个偶数有10个，其中5个是4的倍数。 …………8分
∴P2=1
…………12分
20.(1)连结A1B、A1E，并延长A1E交AC的延长线于点P，连BP由E为C
∵D、E分别是A1B、A1P的中点，
∴DE∥BP
又BP
面ABC，DE
面ABC
∴DE∥平面ABC …………4分
(2)∵△ABC为等腰直角三角形，∠BAC=90°，F为BC的中点
∴BC⊥AF
∵BB1⊥平面ABC，∴B
∴∠B1FB为二面角B1-AF-B的平面角
在Rt△B1BF中，∠B1BF=90°，B1B=a,BF=
∴tan∠B1FB=
∴∠B1FB=arctan
…………8分
即二面β1-AF-B的大小为arctan
(3)∵B
∴B
由AF⊥BC，有AF⊥平面B1BCC1，即AF⊥平面B1EF
∴VF-B1AE=VA-B1EF=
…………12分
(注：用向量解法可参照给分)
21.证：(1)设f(x)上任意两点，A(x1,f(x1)), B(x2,f(x2))不妨令x1>x2
∵
∴f(x1)-f(x2)<x1-x2
即f(x1)-x1<f(x2-x2)令g(x)=f(x)-x=-x3+ax2-x+b
∵当x1>x2时g(x1)<g(x2)
∵g(x)单调递减 ……………6分
(2)∴g(x)单调递减∴g′(x)≤0恒成立
∴-3x2+2ax-1≤0恒成立
∴△=
∴-
≤a≤ ……………12分
22.(1)∵
=(x,y+2) 
=(x,y-2)
||+||=8,∴
=8
由椭圆定义知，M点轨迹是以(0，2)和(0，-2)为焦点的椭圆
∴
……………6分
(2)∵l的斜率一定存在，设l：y=kx+3
(3k2+4)x2+18kx-21=0 ……………8分
设A(x1，y1),B(x2,y2)
∵
∴OAPB为平行四边形
又∵
即OAPB为矩形 ∴
∴x1x2+y1y2=0
∴(1+k2)x1x2+3k(x1+x2)+9=0
∴-(1+k2)?
∴k2=
∴k=±
经检验k=±合题意.
∴存在直线l：y=±x+3 …………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com