
题目列表(包括答案和解析)
(本小题满分12分)
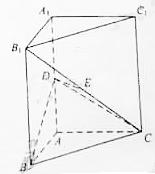
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
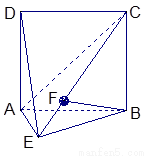
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
(本小题满分12分)如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
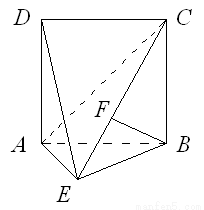
(I)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
(Ⅲ)求点D到平面ACE的距离.
(本小题满分12分)
如图,直二面角D—AB—E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.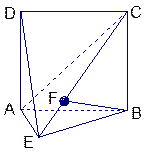
(Ⅰ)求证AE⊥平面BCE;
(Ⅱ)求二面角B—AC—E的大小;
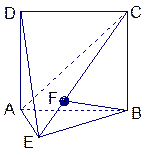
(本小题满分12分)如图,直三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,
的中点,![]() 平面
平面![]()
(I)证明:![]()
(II)设二面角![]() 为60°,求
为60°,求![]() 与平面
与平面![]() 所成的角的大小。
所成的角的大小。
1.A 2.C 3.B 4.A 5.C 6.C 7.D 8.C 9.D 10.B
1l.B 12.A
1.解析:,故选A.
2.解析:
,∴选C.
3.解析:是增函数
故,即
又
,故选B.
4.解析:如图作出可行域,作直线,平移直线至位置,使其经过点.此时目标函数取得最大值(注意与反号)
由得
,故选A
5.解析:设有人投中为事件,则,
故选C.
6.解析:展开式中能项;
由,得,故选C.
7.解析:
由得
,故选D.
8.略
9.解析:由得准线方程,双曲线准线方程为
,解得,
,故选D.
10.解析:设正四面体的棱长为2,取中点为,连接,则为与所成的角,在中
,故选B.
11.解析:由题意,则,故选B.
12.解析:由已知,
为球的直径
,又,
设,则
,
又由,解得
,故选A.
另法:将四面体置于正方休中.
正方体的对角线长为球的直径,由此得,然后可得.
二、
13.解析:在上的投影是.
14.解析:,且.
15.解析:,
由余弦定理为钝角
,即,
解得.
16.
解析:容易知命题①是错的,命题②、③都是对的,对于命题④我们考查如图所示的正方体,设棱长为,显然与为平面内两条距离为的平行直线,它们在底面内的射影、仍为两条距离为的平行直线,但两平面与却是相交的.
三、
17.解:(1),
,
即,故.
(2)
由得.
设边上的高为,则
.
18.(1)设甲、乙两人同时参加灾区服务为事件,则.
(2)记甲、乙两人同时参加同一灾区服务为事件,那么.
(3)随机变量可能取得值为1,2,事件“”是指有两人同时参加灾区服务,则,所以.
分布列是
1
2
19.解:(1)平面
∵二面角为直二面角,且,
平面 平面.
(2)(法一)连接与高交于,连接是边长为2的正方形, ,
二平面,由三垂线定理逆定理得
是二面角的平面角
由(1)平面,
.
在中,
∴在中,
故二面角等于.
(2)(法二)利用向量法,如图以之中点为坐标原点建立空间坐标系,则
,
设平面的法向量分别为,则由
得,而平面的一个法向理
故所求二面角等于.
20.解:(1)由题设,即
易知是首项为、公差为2的等差数列,
∴通项公式为,
(2)由题设,,得是以公比为的等比数列.
由得.
21.解:(1)由题意,由抛物线定义可求得曲线的方程为.
(2)证明:设、的坐标分别为
若直线有斜率时,其坐标满足下列方程组:
,
若没有斜率时,方程为.
又.
;又,
.
22.(1)解:,于是,
解得或
因,故.
(2)证明:已知函数都是奇函数.
所以函数也是奇函数,其图象是以原点为中心的中心对称图形,而.
可知.函数的图象按向量平移,即得到函数的图象,故函数的图象是以点(1,1)为中心的中心对称图形,
(3)证明;在曲线上作取一点,
由知,过此点的切线方程为
.
令,得,切线与直线交点为.
令,得切线与直线交点为,直线与直线与直线的交点为(1,1).
从而所围三角形的面积为
所以,围成三角形的面积为定值2.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com