
题目列表(包括答案和解析)

| ||
| n个6 |
| ||
| (n-1)个6 |
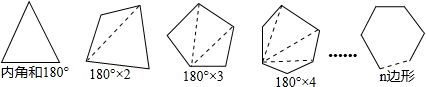

已知任意三角形的内角和为180°,试利用多边形中过某一点的对角线条数,寻求多边形内角和的公式.

根据上图所示,一个四边形可以分成 _________ 个三角形;于是四边形的内角和为 _________ 度:一个五边形可以分成 _________ 个三角形,于是五边形的内角和为 _________ 度,…,按此规律,n边形可以分成_________ 个三角形,于是n边形的内角和为_________ 度.

 =_________.
=_________.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com