
题目列表(包括答案和解析)

阅读下面的题目及分析过程,并按要求进行证明.
已知:如图,E是BC的中点,点A在DE上,且∠BAE=∠CDE.
求证:AB=CD.

分析:证明两条线段相等,常用的一般方法是应用全等三角形或等腰三角形的判定和性质,观察本题中要证明的两条线段,它们不在同一个三角形中,且它们分别所在的两个三角形也不全等.因此,要证AB=CD,必须添加适当的辅助线,构造全等三角形或等腰三角形.
现给出如下三种添加辅助线的方法,请任意选择其中一种,对原题进行证明.

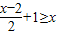 ,并将解集表示在数轴上.
,并将解集表示在数轴上.
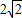 ;
;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com