
题目列表(包括答案和解析)
 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的
支援C粮仓,这时A,B两处粮仓的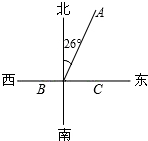 存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)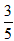 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的存粮吨数相等。(sin26°=0.44,cos26°=0.90,tan26°=0.49)
支援C粮仓,这时A,B两处粮仓的存粮吨数相等。(sin26°=0.44,cos26°=0.90,tan26°=0.49)
 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
 支援C粮仓,从B粮仓运出该粮仓存粮的
支援C粮仓,从B粮仓运出该粮仓存粮的 支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
支援C粮仓,这时A,B两处粮仓的存粮吨数相等.(sin26°=0.44,cos26°=0.90,tan26°=0.49)
一、选择题(每小题2分,共20分)
题 号
1
2
3
4
5
6
7
8
9
10
答 案
A
D
B
A
C
C
B
B
A
A
二、填空题(每小题3分,共24分)
11.x≠-1; 12.60度; 13.-1; 14.4;15.13;16.1或5;17.3-%20(NXPowerLite).files/image092.gif) ;18.136.
;18.136.
19.解:原式=×(1+) =(x+1)()=x+x+1=x+2.
20.解:(1)%20(NXPowerLite).files/image224.gif) ,
,%20(NXPowerLite).files/image226.gif) .
.
(2)%20(NXPowerLite).files/image228.gif) (小时);
(小时);
答:该班学生这一周帮助父母做家务时间的平均数约为1.68小时.
(3)符合实际.设中位数为%20(NXPowerLite).files/image230.gif) ,根据题意,
,根据题意,%20(NXPowerLite).files/image230.gif) 的取值范围是
的取值范围是%20(NXPowerLite).files/image233.gif) ,因为小明帮父母做家务的时间大于中位数.所以他帮父母做家务的时间比班级中一半以上的同学多.
,因为小明帮父母做家务的时间大于中位数.所以他帮父母做家务的时间比班级中一半以上的同学多.
根据题意得:%20(NXPowerLite).files/image238.gif) 解得:
解得:%20(NXPowerLite).files/image240.gif)
(2)A粮仓支援C粮仓的粮食是%20(NXPowerLite).files/image242.gif) (吨)B粮仓支援C粮仓的粮食是
(吨)B粮仓支援C粮仓的粮食是%20(NXPowerLite).files/image244.gif) (吨)
(吨)
A,B两粮仓合计共支援C粮仓粮食为162+72=234吨.∵234>200∴ 此次调拨能满足C粮仓需求.
(3)根据题意知:%20(NXPowerLite).files/image246.gif) ,
,%20(NXPowerLite).files/image248.gif) 千米,
千米,%20(NXPowerLite).files/image250.gif) 在
在%20(NXPowerLite).files/image252.gif) 中,
中,%20(NXPowerLite).files/image254.gif) ,
,
∴BC=AB?sin∠BAC=180×0.44=79.2. ∵此车最多可行驶4×35=140(千米)<2×79.2(千米)
∴小王途中须加油才能安全回到B地.
22.解:(1)由5%20(NXPowerLite).files/image256.gif) =0,得
=0,得%20(NXPowerLite).files/image258.gif) ,
,%20(NXPowerLite).files/image260.gif) .∴抛物线与x轴的交点坐标为(0,0)、(
.∴抛物线与x轴的交点坐标为(0,0)、(%20(NXPowerLite).files/image262.gif) ,0).
,0).
(2)当a=1时,得A(1,17)、B(2,44)、C(3,81),
分别过点A、B、C作x轴的垂线,垂足分别为D、E、F,则有
%20(NXPowerLite).files/image264.gif) =S
=S%20(NXPowerLite).files/image266.gif) -
-%20(NXPowerLite).files/image268.gif) -
-%20(NXPowerLite).files/image270.gif) =
=%20(NXPowerLite).files/image272.gif) -
-%20(NXPowerLite).files/image274.gif) -
-%20(NXPowerLite).files/image276.gif) =5(单位面积)
=5(单位面积)
(3)如:%20(NXPowerLite).files/image278.gif) . 事实上,
. 事实上,%20(NXPowerLite).files/image280.gif) =
=
%20(NXPowerLite).files/image281.gif) 3(
3(%20(NXPowerLite).files/image283.gif) )=3[5×(
)=3[5×(%20(NXPowerLite).files/image278.gif) .
.
23.(1)AB∥CD 证明:分别过点C,D,作CG⊥AB,DH⊥AB,
垂足为G,H,则∠CGA=∠DHB=90°.∴ CG∥DH.
∵ △ABC与△ABD的面积相等, ∴ CG=DH.
∴ 四边形CGHD为平行四边形. ∴ AB∥CD.
%20(NXPowerLite).files/image285.jpg) (2)①证明:连结MF,NE.设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
(2)①证明:连结MF,NE.设点M的坐标为(x1,y1),点N的坐标为(x2,y2).
∵ 点M,N在反比例函数%20(NXPowerLite).files/image170.gif) (k>0)的图象上,∴
(k>0)的图象上,∴ %20(NXPowerLite).files/image288.gif) ,
,%20(NXPowerLite).files/image290.gif) .
.
∵ ME⊥y轴,NF⊥x轴,∴ OE=y1,OF=x2. ∴ S△EFM=%20(NXPowerLite).files/image292.gif) ,
,
S△EFN=%20(NXPowerLite).files/image294.gif) . ∴S△EFM =S△EFN.由(1)中的结论可知:MN∥EF.
. ∴S△EFM =S△EFN.由(1)中的结论可知:MN∥EF.
② MN∥EF. (若学生使用其他方法,只要解法正确,皆给分.)
%20(NXPowerLite).files/image297.gif) 24.解:(1)如图2,点P即为所画点.(答案不唯一.画图正确,无文字说明不扣分;点P画在AC中点不给分)
24.解:(1)如图2,点P即为所画点.(答案不唯一.画图正确,无文字说明不扣分;点P画在AC中点不给分)
(2)如图3,点P即为所作点.(作图正确,无文字说明不扣分;无痕迹或痕迹不清晰的酌情扣分)
(3)连结DB,在△DCF与△BCE中,∠DCF=∠BCE,∠CDF=∠CBE,CF=CE.∴△DCF≌△BCE(AAS),
∴CD=CB,∴∠CDB=∠CBD,∴∠PDB=∠PBD,∴PD=PB,∵PA≠PC.∴点P是四边形ABCD的准等距点.
C
D
总计
A
(240-x)台
(x-40)台
200台
B
x台
(300-x)台
300台
总计
240台
260台
500台
(1)填表
%20(NXPowerLite).files/image303.gif) 依题意得:
依题意得:%20(NXPowerLite).files/image305.gif) . ∴40≤
. ∴40≤%20(NXPowerLite).files/image307.gif) ≤240
≤240
在%20(NXPowerLite).files/image302.gif) 中,∵2>0, ∴
中,∵2>0, ∴%20(NXPowerLite).files/image309.gif) 随
随%20(NXPowerLite).files/image307.gif) 的增大而增大,
的增大而增大,
故当%20(NXPowerLite).files/image307.gif) =40时,总运费最小,此时调运方案为如表一.
=40时,总运费最小,此时调运方案为如表一.
(3)由题意知%20(NXPowerLite).files/image312.gif) ∴0<
∴0<%20(NXPowerLite).files/image179.gif) <2时,(2)中调运方案总运费最小;
<2时,(2)中调运方案总运费最小;%20(NXPowerLite).files/image179.gif) =2时,在
=2时,在
40≤%20(NXPowerLite).files/image307.gif) ≤240的前提下调运,方案的总运费不变;2<
≤240的前提下调运,方案的总运费不变;2<%20(NXPowerLite).files/image179.gif) <15时,
<15时,%20(NXPowerLite).files/image307.gif) =240总运费最小,其调
=240总运费最小,其调
运方案如表二 .
26.解:(1)所求关系式为:%20(NXPowerLite).files/image316.gif) .
.
(2)依题意,%20(NXPowerLite).files/image185.gif) 只能在
只能在%20(NXPowerLite).files/image218.gif) 边上,
边上,%20(NXPowerLite).files/image320.gif) .
. %20(NXPowerLite).files/image322.gif) ,
,
因为%20(NXPowerLite).files/image208.gif) ,所以
,所以%20(NXPowerLite).files/image325.gif) ,三角形相似关系得
,三角形相似关系得%20(NXPowerLite).files/image327.gif) .
.
(3)梯形%20(NXPowerLite).files/image181.gif) 的面积为18. 当
的面积为18. 当%20(NXPowerLite).files/image185.gif) 不在
不在%20(NXPowerLite).files/image218.gif) 边上,则
边上,则%20(NXPowerLite).files/image332.gif) ,
,
(%20(NXPowerLite).files/image112.gif) )当
)当%20(NXPowerLite).files/image335.gif) 时,
时,%20(NXPowerLite).files/image185.gif) 在
在%20(NXPowerLite).files/image338.gif) 边上,
边上,%20(NXPowerLite).files/image340.gif) . 如果线段
. 如果线段%20(NXPowerLite).files/image201.gif) 能平分梯形
能平分梯形%20(NXPowerLite).files/image181.gif) 的面积,则有
的面积,则有%20(NXPowerLite).files/image344.gif) 可得:
可得:%20(NXPowerLite).files/image346.gif) 解得
解得%20(NXPowerLite).files/image348.gif) (
(%20(NXPowerLite).files/image350.gif) 舍去).
舍去).
(%20(NXPowerLite).files/image116.gif) )当
)当%20(NXPowerLite).files/image353.gif) 时,点
时,点%20(NXPowerLite).files/image185.gif) 在
在%20(NXPowerLite).files/image356.gif) 边上,此时
边上,此时%20(NXPowerLite).files/image358.gif) . 如果线段
. 如果线段%20(NXPowerLite).files/image201.gif) 能平分梯形
能平分梯形%20(NXPowerLite).files/image181.gif) 的面积,则有
的面积,则有%20(NXPowerLite).files/image362.gif) , 可得
, 可得%20(NXPowerLite).files/image364.gif) 此方程组无解.
此方程组无解.
所以当%20(NXPowerLite).files/image366.gif) 时,线段
时,线段%20(NXPowerLite).files/image201.gif) 能平分梯形
能平分梯形%20(NXPowerLite).files/image181.gif) 的面积.
的面积.
本资料由《七彩教育网》www.7caiedu.cn 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com