练习册

  • 练习册
  • 试题
    例2.若..则的最大值为 . 【查看更多】

     

    题目列表(包括答案和解析)

    （08年江苏卷）（I）设是各项均不为零的等差数列，且公差，若将此数列删去某一项得到的数列（按原来的顺序）是等比数列：

    （1）①     当时，求的数值；②求的所有可能值；

    （2）求证：对于一个给定的正整数，存在一个各项及公差都不为零的等差数列，其中任意三项（按原来的顺序）都不能组成等比数列。

    查看答案和解析>>

    （08年江苏卷）在平面直角坐标系中，椭圆的焦距为2，以O为圆心，为半径的圆，过点作圆的两切线互相垂直，则离心率=    　▲　　     。

    查看答案和解析>>

    （08年江苏卷） 若，

    且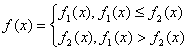

    （1）求对所有实数成立的充要条件（用表示）

    （2）设为两实数，且若

    求证：在区间上的单调增区间的长度和为（闭区间的长度定义为）。

     

    查看答案和解析>>

    （08年江苏卷）某地区为了解70~80岁老人的日平均睡眠时间（单位：h），随机选择了50位老人进行调查。下表是这50位老人日睡眠时间的频率分布表。

    序号

    （i）

    分组

    （睡眠时间）

    组中值（）

    频数

    （人数）

    频率

    （）

    1

    [4,5)

    4.5

    6

    0.12

      2

    [5,6)

    5.5

    10

    0.20

    3

    [6,7)

    6.5

    20

    0.40

    4

    [7,8)

    7.5

    10

    0.20

    5

    [8,9)

    8.5

    4

    0.08

    在上述统计数据的分析中，一部分计算算法流程图，则输出的S的值是     ▲         。

    查看答案和解析>>

    （08年江苏卷）一个骰子连续投2次，点数和为4的概率为          ▲        。

    查看答案和解析>>

    1. 构造向量，，所以，.由数量积的性质，得，即的最大值为2.

    2. ∵，令得，所以，当时，，当时，，所以当时，.

    3.∵，∴，，又，∴，则，所以周期.作出在上的图象知：若，满足条件的（）存在，且，关于直线对称，，关于直线对称，∴；若，满足条件的（）存在，且，关于直线对称，，关于直线对称，

    ∴. 

    4. 不等式（）表示的区域是如图所示的菱形的内部，

    ∵，

    当，点到点的距离最大，此时的最大值为；

    当，点到点的距离最大，此时的最大值为3.

    5. 由于已有两人分别抽到5和14两张卡片，则另外两人只需从剩下的18张卡片中抽取，共有种情况.抽到5 和14的两人在同一组，有两种情况:

    (1) 5 和14 为较小两数，则另两人需从15～20这6张中各抽1张,有种情况；

    (2) 5 和14 为较大两数，则另两人需从1～4这4张中各抽1张,有种情况.

    于是，抽到5 和14 两张卡片的两人在同一组的概率为.

    6. ∵，∴，

    设，，则.

    作出该不等式组表示的平面区域（图中的阴影部分）.

    令，则，它表示斜率为的一组平行直线，易知，当它经过点时，取得最小值.

    解方程组，得，∴


    同步练习册答案