(本题满分14分)

如图，将一次函数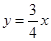的图象上一点A(a，b)，沿竖直方向向上移动6个单位，得到点B，再沿水平方向向右移动8个单位，得到点C．以AC为直径作圆E，设垂直于y轴的直线DT与圆E相切于点D．

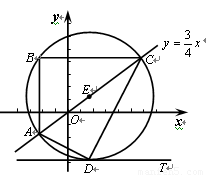
1.(1) 求证：点C在一次函数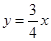的图象上；

2.(2) 求三角形ADC的面积；

3.(3) 当点D在x轴上时，求点A的坐标．

(本题满分14分)
如图是某市一条河上一座古拱挢的截面图，拱桥桥洞上沿是抛物线形状，抛物线拱桥处于正常水位时水面宽AB为26m，当水位上涨1m时，抛物线拱桥的水面宽CD为24m．现以水面AB所在直线为x轴，抛物线的对称轴为y轴建立直角坐标系．

【小题1】(1) 求出抛物线的解析式；
【小题2】(2) 经过测算，水面离拱桥顶端1.5m时为警戒水位．某次洪水到来时，小明用仪器测得水面宽为10m，请你帮助小明算一算，此时水面是否超过警戒水位．

(本题满分14分)

如图是某市一条河上一座古拱挢的截面图，拱桥桥洞上沿是抛物线形状，抛物线拱桥处于正常水位时水面宽AB为26m，当水位上涨1m时，抛物线拱桥的水面宽CD为24m．现以水面AB所在直线为x轴，抛物线的对称轴为y轴建立直角坐标系．

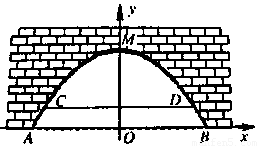
1.(1) 求出抛物线的解析式；

2.(2) 经过测算，水面离拱桥顶端1.5m时为警戒水位．某次洪水到来时，小明用仪器测得水面宽为10m，请你帮助小明算一算，此时水面是否超过警戒水位．

(本题满分14分)
如图，将一次函数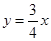的图象上一点A(a，b)，沿竖直方向向上移动6个单位，得到点B，再沿水平方向向右移动8个单位，得到点C．以AC为直径作圆E，设垂直于y轴的直线DT与圆E相切于点D．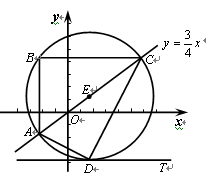

【小题1】(1) 求证：点C在一次函数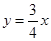的图象上；
【小题2】(2) 求三角形ADC的面积；
【小题3】(3) 当点D在x轴上时，求点A的坐标．

(本题满分14分)

如图是某市一条河上一座古拱挢的截面图，拱桥桥洞上沿是抛物线形状，抛物线拱桥处于正常水位时水面宽AB为26m，当水位上涨1m时，抛物线拱桥的水面宽CD为24m．现以水面AB所在直线为x轴，抛物线的对称轴为y轴建立直角坐标系．

1.(1) 求出抛物线的解析式；

2.(2) 经过测算，水面离拱桥顶端1.5m时为警戒水位．某次洪水到来时，小明用仪器测得水面宽为10m，请你帮助小明算一算，此时水面是否超过警戒水位．