
题目列表(包括答案和解析)
设函数 ,若
,若 为函数
为函数 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为 的图象是
的图象是

【答案】D
【解析】设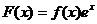 ,∴
,∴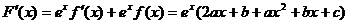 ,
,
又∴ 为
为 的一个极值点,
的一个极值点,
∴ ,即
,即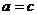 ,
,
∴ ,
,
当 时,
时, ,即对称轴所在直线方程为
,即对称轴所在直线方程为 ;
;
当 时,
时, ,即对称轴所在直线方程应大于1或小于-1.
,即对称轴所在直线方程应大于1或小于-1.
设抛物线 :
: (
( >0)的焦点为
>0)的焦点为 ,准线为
,准线为 ,
, 为
为 上一点,已知以
上一点,已知以 为圆心,
为圆心, 为半径的圆
为半径的圆 交
交 于
于 ,
, 两点.
两点.
(Ⅰ)若 ,
, 的面积为
的面积为 ,求
,求 的值及圆
的值及圆 的方程;
的方程;
(Ⅱ)若 ,
, ,
, 三点在同一条直线
三点在同一条直线 上,直线
上,直线 与
与 平行,且
平行,且 与
与 只有一个公共点,求坐标原点到
只有一个公共点,求坐标原点到 ,
, 距离的比值.
距离的比值.
【命题意图】本题主要考查圆的方程、抛物线的定义、直线与抛物线的位置关系、点到直线距离公式、线线平行等基础知识,考查数形结合思想和运算求解能力.
【解析】设准线 于
于 轴的焦点为E,圆F的半径为
轴的焦点为E,圆F的半径为 ,
,

则|FE|= ,
, =
= ,E是BD的中点,
,E是BD的中点,
(Ⅰ) ∵ ,∴
,∴ =
= ,|BD|=
,|BD|= ,
,
设A( ,
, ),根据抛物线定义得,|FA|=
),根据抛物线定义得,|FA|= ,
,
∵ 的面积为
的面积为 ,∴
,∴ =
= =
= =
= ,解得
,解得 =2,
=2,
∴F(0,1), FA|= , ∴圆F的方程为:
, ∴圆F的方程为: ;
;
(Ⅱ) 解析1∵ ,
, ,
, 三点在同一条直线
三点在同一条直线 上, ∴
上, ∴ 是圆
是圆 的直径,
的直径, ,
,
由抛物线定义知 ,∴
,∴ ,∴
,∴ 的斜率为
的斜率为 或-
或- ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
设直线 的方程为:
的方程为: ,代入
,代入 得,
得, ,
,
∵ 与
与 只有一个公共点,
∴
只有一个公共点,
∴ =
= ,∴
,∴ ,
,
∴直线 的方程为:
的方程为: ,∴原点到直线
,∴原点到直线 的距离
的距离 =
= ,
,
∴坐标原点到 ,
, 距离的比值为3.
距离的比值为3.
解析2由对称性设 ,则
,则
点 关于点
关于点 对称得:
对称得:
得: ,直线
,直线
 切点
切点
直线
坐标原点到 距离的比值为
距离的比值为
等轴双曲线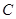 的中心在原点,焦点在
的中心在原点,焦点在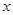 轴上,
轴上,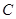 与抛物线
与抛物线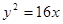 的准线交于
的准线交于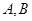 两点,
两点,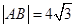 ;则
;则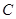 的实轴长为( )
的实轴长为( )
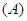
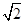
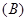
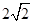

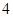
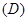
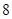
【解析】设等轴双曲线方程为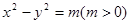 ,抛物线的准线为
,抛物线的准线为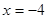 ,由
,由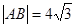 ,则
,则 ,把坐标
,把坐标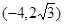 代入双曲线方程得
代入双曲线方程得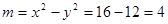 ,所以双曲线方程为
,所以双曲线方程为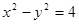 ,即
,即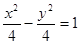 ,所以
,所以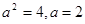 ,所以实轴长
,所以实轴长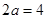 ,选C.
,选C.
设函数f(x)= 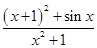 的最大值为M,最小值为m,则M+m=____
的最大值为M,最小值为m,则M+m=____
【解析】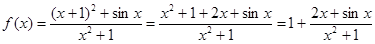 ,令
,令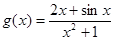 ,则
,则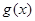 为奇函数,对于一个奇函数来说,其最大值与最小值之和为0,即
为奇函数,对于一个奇函数来说,其最大值与最小值之和为0,即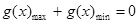 ,而
,而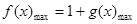 ,
,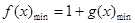 ,所以
,所以 .
.
如图,直线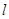 与抛物线
与抛物线 交于
交于 两点,与
两点,与 轴相交于点
轴相交于点 ,且
,且 .
.
(1)求证: 点的坐标为
点的坐标为 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com