
题目列表(包括答案和解析)
已知 ,
,
求  和
和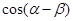 的值.
的值.
【解析】利用三角恒等变换得到函数值,
由于
得

解析: 由

得

已知在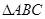 中,
中,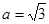 ,
,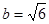 ,
,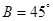 ,解这个三角形;
,解这个三角形;
【解析】本试题主要考查了正弦定理的运用。由正弦定理得到: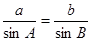
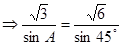 ,然后又
,然后又 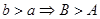
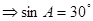
又 再又
再又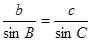 得到c。
得到c。
解:由正弦定理得到: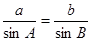
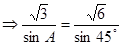
又 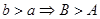
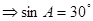 ……4分
……4分
又 ……8分
……8分
又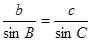
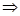
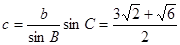
求由抛物线 与直线
与直线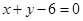 及
及 所围成图形的面积.
所围成图形的面积.
【解析】首先利用已知函数和抛物线作图,然后确定交点坐标,然后利用定积分表示出面积为 ,所以得到
,所以得到 ,由此得到结论为
,由此得到结论为
解:设所求图形面积为 ,则
,则

 =
= .即所求图形面积为
.即所求图形面积为 .
.

已知指数函数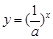 ,当
,当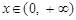 时,有
时,有 ,解关于x的不等式
,解关于x的不等式
【解析】本试题主要考查了指数函数,对数函数性质的运用。首先利用指数函数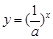 ,当
,当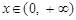 时,有
时,有 ,,得到
,,得到 ,从而
,从而
 等价于
等价于 ,联立不等式组可以解得
,联立不等式组可以解得
解:∵ 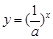 在
在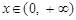 时,有
时,有 ,
∴
,
∴  。
。
于是由 ,得
,得 ,
,
解得 ,
∴ 不等式的解集为
,
∴ 不等式的解集为 。
。
已知 ,(其中
,(其中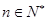 )
)
⑴求 及
及 ;
;
⑵试比较 与
与 的大小,并说明理由.
的大小,并说明理由.
【解析】第一问中取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得
取 ,则
,则 得到结论
得到结论
第二问中,要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,归纳猜想可得结论当
的大小,归纳猜想可得结论当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
;
猜想:当 时,
时, 运用数学归纳法证明即可。
运用数学归纳法证明即可。
解:⑴取 ,则
,则 ;
…………1分
;
…………1分
对等式两边求导,得 ,
,
取 ,则
,则 。 …………4分
。 …………4分
⑵要比较 与
与 的大小,即比较:
的大小,即比较: 与
与 的大小,
的大小,
当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时, ;
…………6分
;
…………6分
猜想:当 时,
时, ,下面用数学归纳法证明:
,下面用数学归纳法证明:
由上述过程可知, 时结论成立,
时结论成立,
假设当 时结论成立,即
时结论成立,即 ,
,
当 时,
时,
而
∴
即 时结论也成立,
时结论也成立,
∴当 时,
时, 成立。
…………11分
成立。
…………11分
综上得,当 时,
时, ;
;
当 时,
时, ;
;
当 时,
时,
1. 构造向量 ,
, ,所以
,所以 ,
, .由数量积的性质
.由数量积的性质 ,得
,得 ,即
,即 的最大值为2.
的最大值为2.
2. ∵ ,令
,令 得
得 ,所以
,所以 ,当
,当 时,
时, ,当
,当 时,
时, ,所以当
,所以当 时,
时, .
.
3.∵ ,∴
,∴ ,
, ,又
,又 ,∴
,∴ ,则
,则 ,所以周期
,所以周期 .作出
.作出 在
在 上的图象知:若
上的图象知:若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,∴
对称,∴ ;若
;若 ,满足条件的
,满足条件的 (
( )存在,且
)存在,且 ,
, 关于直线
关于直线 对称,
对称, ,
, 关于直线
关于直线 对称,
对称,
 ∴
∴ .
.
4. 不等式 (
( )表示的区域是如图所示的菱形的内部,
)表示的区域是如图所示的菱形的内部,
∵
 ,
,
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为
的最大值为 ;
;
当 ,点
,点 到点
到点 的距离最大,此时
的距离最大,此时 的最大值为3.
的最大值为3.
5. 由于已有两人分别抽到5和14两张卡片,则另外两人只需从剩下的18张卡片中抽取,共有 种情况.抽到5 和14的两人在同一组,有两种情况:
种情况.抽到5 和14的两人在同一组,有两种情况:
(1) 5 和14 为较小两数,则另两人需从15~20这6张中各抽1张,有 种情况;
种情况;
(2) 5 和14 为较大两数,则另两人需从1~4这4张中各抽1张,有 种情况.
种情况.
于是,抽到5 和14 两张卡片的两人在同一组的概率为 .
.
 6. ∵
6. ∵ ,∴
,∴ ,
,
设 ,
, ,则
,则 .
.
作出该不等式组表示的平面区域(图中的阴影部分 ).
).
令 ,则
,则 ,它表示斜率为
,它表示斜率为 的一组平行直线,易知,当它经过点
的一组平行直线,易知,当它经过点 时,
时, 取得最小值.
取得最小值.
解方程组 ,得
,得 ,∴
,∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com