张华与李明在讨论问题：“已知线段a、b，求作Rt△ABC，使∠C＝90°，AB＝a，AC=b”时，提出了如下的画法：1、画线段AB＝a；2、以AB为直径画⊙O；3、以A为圆心，b为半径画圆与⊙O交于点C，连接BC，则△ABC为所求作的三角形.

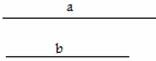
问题1：在张华的画法中，他应用了什么知识得到∠C＝90°的？

答：

问题2：已知△ABC中，∠ACB＝90°，AC＝BC＝2，P、Q分别是边AB、BC上的动点，且点P不与A、B重合，点Q不与B、C重合，当CQ的长取不同的值时，

△CPQ是否可能为直角三角形？若可能，请求出CQ的范围；若不能，说明理由．

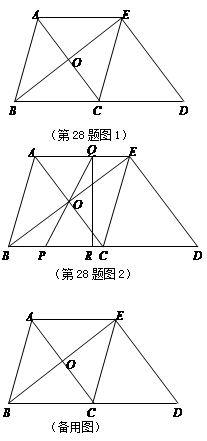
（本题满分10分）如图1，在△ABC中，AB＝BC＝5，AC=6. △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.

（1）判断四边形ABCE是怎样的四边形，说明理由；

（2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.

①四边形PQED的面积是否随点P的运动而发生变化？

若变化，请说明理由；若不变，求出四边形PQED的面积；

②当线段BP的长为何值时，△PQR与△BOC相似？

（本题满分10分）如图1，在△ABC中，AB＝BC＝5，AC="6." △ECD是△ABC沿BC方向平移得到的，连接AE.AC和BE相交于点O.

（1）判断四边形ABCE是怎样的四边形，说明理由；
（2）如图2，P是线段BC上一动点（图2），（不与点B、C重合），连接PO并延长交线段AE于点Q，QR⊥BD，垂足为点R.
①四边形PQED的面积是否随点P的运动而发生变化？
若变化，请说明理由；若不变，求出四边形PQED的面积；
②当线段BP的长为何值时，△PQR与△BOC相似？

（本题满分10分）如图，放置在水平桌面上的台灯的灯臂AB长为40cm，灯

罩BC长为30cm，底座厚度为2cm，灯臂与底座构成的∠BAD=60°. 使用发现，光线最

佳时灯罩BC与水平线所成的角为30°，此时灯罩顶端C到桌面的高度CE是多少cm？