
题目列表(包括答案和解析)
 14、完形填空:
14、完形填空: 推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.
推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.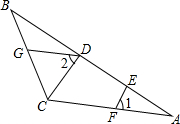 推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.
推理填空:已知:如图,DG∥AC,EF⊥AB,∠1=∠2.求证:CD⊥AB.已知:如图,正方形ABCD的边长为a,BM,DN分别平分正方形的两个外角,且满足
![]() ,连结MC,NC,MN.
,连结MC,NC,MN.

1.(1)填空:与△ABM相似的三角形是△ ,![]() = ;(用含a的代数式表示)
= ;(用含a的代数式表示)
2.(2)求![]() 的度数;
的度数;
3.(3)猜想线段BM,DN和MN之间的等量关系并证明你的结论.
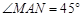 ,连结MC,NC,MN.
,连结MC,NC,MN.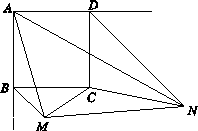
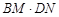 = ;(用含a的代数式表示)
= ;(用含a的代数式表示)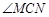 的度数;
的度数;湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com