
题目列表(包括答案和解析)
(本小题满分10分)
如图(1),在平面直角坐标系中,△OAB三个顶点坐标分别为O(0,0),A(1,),B(4,0).
(1)求证:AB⊥OA
(2)在第一象限内确定点M,使△MOB与△AOB相似,求符合条件的点M的坐标.
(3)如图(2),已知D(0,-3),作直线BD.
①将△AOB沿射线BD平移4个单位长度后,求△AOB与以D为圆心,以1为半径的⊙D的公共点的个数.
②如图(3),现有一点P从D点出发,沿射线DB的方向以1个单位长度/秒的速度作匀速运动,运动时间为秒.当以P为圆心,以
为半径的⊙P与△AOB有公共点时,求
的取值范围.
(本小题满分10分)
如图(1),在平面直角坐标系中,△OAB三个顶点坐标分别为O(0,0),A(1,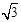 ),B(4,0).
),B(4,0).

(1)求证:AB⊥OA
(2)在第一象限内确定点M,使△MOB与△AOB相似,求符合条件的点M的坐标.
(3)如图(2),已知D(0,-3),作直线BD.
①将△AOB沿射线BD平移4个单位长度后,求△AOB与以D为圆心,以1为半径的⊙D的公共点的个数.
②如图(3),现有一点P从D点出发,沿射线DB的方向以1个单位长度/秒的速度作匀速运动,运动时间为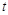 秒.当以P为圆心,以
秒.当以P为圆心,以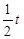 为半径的⊙P与△AOB有公共点时,求
为半径的⊙P与△AOB有公共点时,求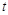 的取值范围.
的取值范围.
如图①,△ABC中,AB=BC,∠B=90°,点A,B的坐标分别(0,10),(8,4),点C在 第一象限.动点P从点A出发沿边AB―BC匀速运动,同时动点Q以相同的速度在x轴上运动,图②是当点P在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象.
(1)求点P、Q运动的速度;
(2)求点C的坐标;
(3)求点P在边AB上运动时,△OPQ的面积S(平方单位)关于时间t(秒)的函数关系式,并求当点P运动到边AB上哪个位置时,△OPQ的面积最大?
(4)(本小题为选做题,做对另加3分,但全卷满分不超过150分)已知点P在边AB上运动时,∠OPQ的大小随时间t的增大而增大,点P在边BC上运动时,∠OPQ的大小随时间t的增大而减小,那么当点P在这两边上运动时,使∠OPQ =90°的点P有
______个(只填结论,不需解答过程).

图 ① 图②
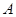 、
、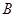 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往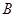 城,乙车驶往
城,乙车驶往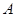 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距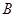 城高速公路入口处的距离
城高速公路入口处的距离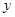 (千米)与行驶时间
(千米)与行驶时间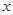 (时)之间的关系如图.
(时)之间的关系如图.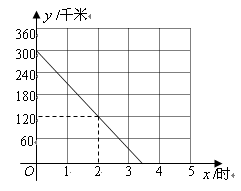
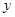 关于
关于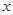 的表达式;
的表达式;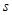 (千米).请直接写出
(千米).请直接写出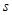 关于
关于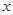 的表达式;
的表达式;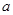 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度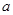 .在下图中画出乙车离开
.在下图中画出乙车离开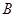 城高速公路入口处的距离
城高速公路入口处的距离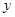 (千米)与行驶时间
(千米)与行驶时间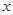 (时)之间的函数图象.
(时)之间的函数图象.(本题满分10分)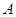 、
、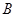 两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往
两座城市之间有一条高速公路,甲、乙两辆汽车同时分别从这条路两端的入口处驶入,并始终在高速公路上正常行驶.甲车驶往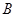 城,乙车驶往
城,乙车驶往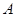 城,甲车在行驶过程中速度始终不变.甲车距
城,甲车在行驶过程中速度始终不变.甲车距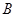 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间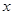 (时)之间的关系如图.
(时)之间的关系如图.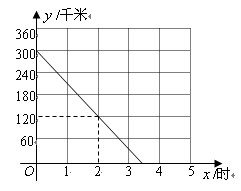
【小题1】(1)求 关于
关于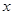 的表达式;
的表达式;
【小题2】(2)已知乙车以60千米/时的速度匀速行驶,设行驶过程中,相遇前两车相距的路程为 (千米).请直接写出
(千米).请直接写出 关于
关于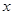 的表达式;
的表达式;
【小题3】(3)当乙车按(2)中的状态行驶与甲车相遇后,速度随即改为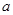 (千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度
(千米/时)并保持匀速行驶,结果比甲车晚40分钟到达终点,求乙车变化后的速度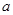 .在下图中画出乙车离开
.在下图中画出乙车离开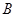 城高速公路入口处的距离
城高速公路入口处的距离 (千米)与行驶时间
(千米)与行驶时间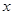 (时)之间的函数图象.
(时)之间的函数图象.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com