
题目列表(包括答案和解析)
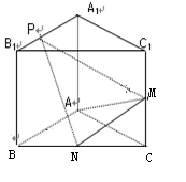
如图,已知三棱锥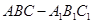 的侧棱与底面垂直,
的侧棱与底面垂直,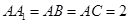 ,
,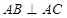 , M、N分别是
, M、N分别是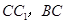 的中点,点P在线段
的中点,点P在线段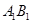 上,且
上,且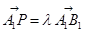 ,
,
(1)证明:无论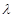 取何值,总有
取何值,总有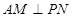 .
.
(2)当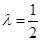 时,求平面
时,求平面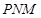 与平面
与平面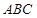 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段 上,且
上,且 ,
,
 取何值,总有
取何值,总有 .
. 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.如图,已知三棱锥 的侧棱与底面垂直,
的侧棱与底面垂直, ,
, , M、N分别是
, M、N分别是 的中点,点P在线段
的中点,点P在线段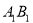 上,且
上,且 ,
,
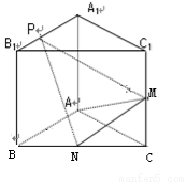
(1)证明:无论 取何值,总有
取何值,总有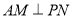 .
.
(2)当 时,求平面
时,求平面 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
已知三棱锥![]() 中,顶点
中,顶点![]() 在底面的射影
在底面的射影![]() 是三角形
是三角形![]() 的内心,关于这个三棱锥有三个命题:①侧棱
的内心,关于这个三棱锥有三个命题:①侧棱![]() ;②侧棱
;②侧棱![]() 两两垂直;③各侧面与底面所成的二面角相等。其中错误的是
两两垂直;③各侧面与底面所成的二面角相等。其中错误的是
已知三棱锥P-ABC中,有PA=BC,PB=AC,PC=AB,三个侧面与底面所成的二面角为α1、α2、α3,则cosα1+cosα2+cosα3=________.
1. 由函数 知,当
知,当 时,
时, ,且
,且 ,则它的反函数过点(3,4),故选A.
,则它的反函数过点(3,4),故选A.
2.∵ ,∴
,∴ ,则
,则 ,即
,即 ,
, .
. ,选B.
,选B.
3. 由平行四边形法则, ,
,
∴ ,
,
又 ,
,
∴ ,当P为
,当P为 中点时,取得最小值
中点时,取得最小值 .选B.
.选B.
4. 设 是椭圆的一个焦点,它是椭圆三个顶点
是椭圆的一个焦点,它是椭圆三个顶点 ,
, ,
, 构成的三角形的垂心(如图).由
构成的三角形的垂心(如图).由 有
有 ,即
,即 ,∴
,∴ ,得
,得 ,解得
,解得 ,选A.
,选A.
5. 设正方形边长为 ,
, ,则
,则 ,
, .在
.在 由正弦定理得
由正弦定理得
 ,又在
,又在 由余弦定理得
由余弦定理得 ,于是
,于是 ,
, ,选C.
,选C.
 6.
6.  在底面
在底面 上的射影
上的射影 知,
知, 为斜线
为斜线 在平面
在平面 上的射影,∵
上的射影,∵ ,由三垂线定理得
,由三垂线定理得 ,∵
,∵ ,所以直线
,所以直线 与直线
与直线 重合,选A.
重合,选A.
7. 过A作抛物线 的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线
的准线的垂线AA1交准线A1,
过B作椭圆的右准线的垂线 交右准线于
交右准线于 则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长
则有:BN=e|BB1|=2-xB,AN=|AA1|=xA+1,周长 =|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
=|AN|+|AB|+|BN|=xA+1+(xB-xA)+(2-xB)=3+xB,
由可得两曲线的交点x=,xB∈(,2),
∴3+xB∈(,4),即△ANB周长 取值范围是(,4),选B.
取值范围是(,4),选B.
8. 先将3,5两个奇数排好,有 种排法,再将4,6两个偶数插入3,5中,有
种排法,再将4,6两个偶数插入3,5中,有 种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为
种排法,最后将1,2 当成一个整体插入5个空位中,所以这样的六位数的个数为 ,选B.
,选B.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com