
题目列表(包括答案和解析)
如图,第①个多边形是由正三角形“扩展”而来的,边数记为![]() ,第②个多边形是由正方形“扩展”而来的,边数记为
,第②个多边形是由正方形“扩展”而来的,边数记为![]() ,…,依次类推,由正
,…,依次类推,由正![]() 边形“扩展”而来的多边形的边数记为
边形“扩展”而来的多边形的边数记为![]() (
(![]() ),则
),则![]() 的值是 ▲ .
的值是 ▲ .
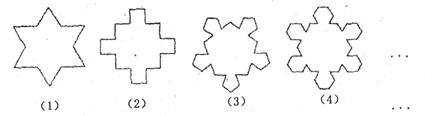
如图,第①个多边形是由正三角形“扩展”而来的,边数记为 ,第②个多边形是由正方形“扩展”而来的,边数记为
,第②个多边形是由正方形“扩展”而来的,边数记为 ,…,依次类推,由正
,…,依次类推,由正 边形“扩展”而来的多边形的边数记为
边形“扩展”而来的多边形的边数记为 (
( ),则
),则 的值是 ▲ .
的值是 ▲ .

如图,第①个多边形是由正三角形“扩展”而来的,边数记为 ,第②个多边形是由正方形“扩展”而来的,边数记为
,第②个多边形是由正方形“扩展”而来的,边数记为 ,…,依次类推,由正
,…,依次类推,由正 边形“扩展”而来的多边形的边数记为
边形“扩展”而来的多边形的边数记为 (
( ),则
),则 的值是 ▲ .
的值是 ▲ .
| 1 |
| a3 |
| 1 |
| an |
| 98 |
| 303 |

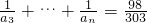 时,则n=______.
时,则n=______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com