题目列表(包括答案和解析)
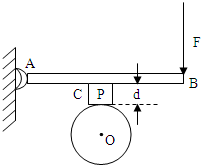如图是电动砂轮打磨工件的装置，砂轮的转轴通过图中O点垂直与纸面，AB是一根长度为0.6m、质量为m1=0.5kg的均匀刚性细杆，可绕过A点的固定轴无摩擦的转动，工件C固定在AB杆上，其质量m2=1.5kg，工件的重心，工件与砂轮的接触点P以及O点都在过AB中心的垂直线上，P到AB杆的垂直距离d=0.01m，AB杆始终处于水平位置．砂轮与工件之间的滑动摩擦系数μ=0.6．
| l |
| 2 |
| l |
| 2 |
| 1 |
| 2 |
| d |
| l |
| l |
| 2 |
| l |
| 2 |
| 1 |
| 2 |
| d |
| l |
高考真题
1．【解析】由合力与分的关系可知,合力最大应是它们同向,最小应是它们反向
【答案】B
2．【解析】重力是地球的吸引而产生的,地球上一切物体都受到重力,与物体的运动状态无关,重力的方向是竖直向下
【答案】D
3．【解析】如图所示，力F产生了两个作用效果，一个是使B压紧竖直墙面的力F1，一个是压紧A的力F2，用整体法进行分析，可知F1和F3的大小相等，当力F缓慢增大时，合力的方向和两个分力的方向都没有发生变化，所以当合力增大时两个分力同时增大，C正确
【答案】C
4．【解析】将力F进行分解,再由整体法在竖直方向运用平衡
条件可列式：Fsinθ＋N=mg＋Mg，则N= mg＋Mg－Fsinθ
【答案】D
5．【解析】竖直挂时
，当质量为2m放到斜面上时，
，因两次时长度一样，所以
也一样。解这两个方程可得，物体受到的摩擦力为零，A正确。
【答案】A
6．【解析】设刚性细杆中弹力为F，光滑的半球面对小球a的弹力为Fa，对小球b的弹力为Fb，分别隔离小球a和b对其分析受力并应用平行四边形定则画出受力分析。由细杆长度是球面半径的倍可得出三角形Oab是直角三角形，∠Oab=∠Oba=45°。对△bFB应用正弦定理得两式联立消去F得sin（45°+θ）= sin（45°―θ）
显然细杆与水平面的夹角θ=15°，正确选项是D。
【答案】D
7．【解析】考查牛顿运动定律。设减少的质量为△m，匀速下降时：Mg=F＋kv，匀速上升时：Mg－△mg＋kv = F，解得△mg = 2(M－)，A正确。
【答案】A
8．【解析】⑴空载时合力为零：
已知：fB＝2fA 求得：fA＝200 kN fB＝400 kN
设机架重心在中心线右侧，离中心线的距离为x，以A为转轴
求得：x＝1.5 m
⑵以A为转轴，力矩平衡
求得：FB＝450 kN
【答案】(1)x＝1.5 m;(2)B＝450 kN
9．【解析】读数时应估读一位，所以其中l5 、 l6两个数值在记录时有误
【答案】①l5 ；l6；②6.85(6.84-6.86) ；14.05(14.04-14.06)；
③l7－l3 ；7.20(7.18-7.22) ；④
名校试题
1．【解析】 猴子受重力和两个拉力人作用，所以选项A正确；两拉力的合力与重力平衡，B错；地球对猴子的引力与猴子对地球的引力是一对作用力和反作用力，C正确；猴子静止合力总为零，选项D错
2．【解析】由力的三角形定则，在重力不变的情况下，
、
和重力构成一个封闭的三角形，从而得到、均减小
【答案】A
3．【解析】由受力分析和摩擦力的产生条件可得选项C正确
【答案】C
4．【解析】由图可知弹簧先压缩后伸长，当弹簧的长度为6cm时，弹力为零，所以弹簧的原长为6cm；当弹簧伸长2cm时，弹力为2N，故弹簧的劲度系数为100N/m
【答案】BC
5．【解析】 隔离物体B可知，绳的张力不变，所以选项A错；隔离物体A得选项D正确
【答案】D
6．【解析】 以整体为研究对象，设斜面的倾角为
，则F3
，是个定值不变；隔离球乙，求得F1缓慢减小．
【答案】D
7．【解析】（1）输电线线冰层的体积V冰 = πR2L
由对称关系可知，塔尖所受压力的增加值等于一根导线上冰层的重力，即
ΔN = ρV冰 g= πρR2Lg
（2）输电线与冰层的总质量M' = m0L + πρR2Lg，输电线受力如图甲所示。
由共点力的平衡条件，得2F1cosθ = m0Lg + πρR2Lg
输电线在最高点所受的拉力
半根输电线的受力如图乙所示。
由共点力的平衡条件，得F2 = F1sinθ
【答案】（1）πρR2Lg；（2）
8．【解析】⑴根据实验数据在坐标纸上描出的点，基本上在同一条直线上。可以判定F和L间是一次函数关系。画一条直线，使尽可能多的点落在这条直线上，不在直线上的点均匀地分布在直线两侧。（5分）
由
可得k=25N/m。
【答案】k=25N/m。
9．【解析】不正确。 平行于斜面的皮带对圆柱体也有力的作用。
（1）式应改为：Fcosβ+F=mgsinα ②
由②得
30N=10N ③
将③代入②得FN=mgcosα－Fsinβ=30×0.8－10×0.6N=18N ④
【答案】18N
10．【解析】原来匀速时F1=
（1）当F2为推力且与F1夹角为时，有
因为F2=F1，解得
(2)当F2为拉力且与水平方向成角时，有
综上所述，当力F2与F1在同一竖直平面内，力F2的方向与力F1的夹角为arccotu或
【答案】
11．【解析】对B球，受力分析如图所示。
Tcos300=NAsin300 ………….①
∴ T=2mg
对A球，受力分析如图D-1所示。在水平方向
Tcos300=NAsin300 …………………..②
在竖直方向
NAcos300=mAg+Tsin300 …………………③
【答案】由以上方程解得：mA=2m
考点预测题
1．【解析】滑动摩擦力F的大小跟物体的相对运动速度的大小没有关系．本题选项为AB
【答案】AB.
2．【解析】本题的立意在考查滑动摩擦力方向的判断，物体A在水平方向有相对圆柱体向左的速度υ′，υ′ = ωr = 1.8m/s；在竖直方向有相对圆柱体向下的速度υ0 = 2.4m/s，所以综合起来A相对于圆柱体的合速度为v，如图18右所示，且υ= = 3m/s?
合速度与竖直方向的夹角为θ，则cosθ = =
A做匀速运动，其受力如图18左所示
图18
竖直方向平衡，有Ff cosθ = mg，得Ff = = 12.5N?另Ff =μFN，FN =F，故F = 
= 50N
【答案】50N
3．【解析】由题给条件知未施加力F时，弹簧的弹力大小为
物块A与地面间的滑动摩擦力大小为
物块B与地面间的滑动摩擦力大小为
令施加力F后装置仍处于静止状态，B受地面的摩擦力为fB，A受地面的摩擦力为fA，由平衡条件有：
，
代入数据解得：
，
因
，表明物块B的确仍处于静止状态。
综合以上分析可知，所给选项中只有C项正确。
【答案】C
4．【解析】此题材把四种不同的物理情景的弹簧放在一起，让学生判别弹簧的伸长量的大小，实际上就是判断四种情景下弹簧所受弹力的大小。由于弹簧的质量不计，所以不论弹簧做何种运动，弹簧各处的弹力大小都相等。因此这情况下弹簧的弹力是相等，即四个弹簧的伸长量是相等。只有D选项正确。
【答案】D
5．【解析】在水对大坝压力一定的情况下，A图所示，为晾衣绳原理中最大情况，即大坝受力最大。固不是最佳方案，而B图与C、D图的区别在于：B图大坝所受压力传递给坝墩，而C、D图所受压力将直接作用在在坝上，受力分析，如图22所示，所以该题选B。
图22
【答案】B
6．【解析】（1）设c′点受两边绳的张力为T1和T2，
的夹角为θ，如图所示。依对称性有：T1=T2=T 由力的合成有 ：
而
=90
-
所以 F=2Tsinθ
根据几何关系有 sinθ=
联立上述二式解得 T=
，因d<<L，故 
（2）将d=10mm，F=400N，L=250mm代入，解得 T=2.5×103N
， 即绳中的张力为2.5×103N
【答案】2.5×103N
7．【解析】因为物体处于静止状态，根据受力平衡得正确答案为C。
【答案】C
8．【解析】设绳子的拉力为F
，将P。Q看作一个整体进行受力分析，整体受两绳相等的拉力和地面的摩擦力做匀速运动，故有 F=2 F+2μmg隔离物体Q由平衡条件有：F=μmg，代入F得：F=4μmg。所以选项A正确。
【答案】A
9．【解析】物体P静止不动，轻绳上拉力和P的重力平衡，故轻绳上拉力一定不变，D项正确。若开始时，Q有下滑趋势，静摩擦力沿斜面向上，用水平恒力向左推Q，则静摩擦力减小；若开始时，Q有上滑趋势，静摩擦力沿斜面向下，用水平恒力向左推Q，则静摩擦力增大。因此，Q受到的摩擦力大小不确定。所以选项D正确
【答案】D
10．【解析】本题的难点是判断硬杆对C点弹力的方向，不少学生认为该力的方向应沿C点杆的切线方向，而不是沿BC方向。若是以杆为研究对象，杆只受到两个力（因为杆的质量忽略不计）；即两个端点对杆的作用力，杆处于平衡，这两个力一定是一对平衡力，若是C点的力不经过B点，那么这两个力不在一条直线上，肯定不是一对平衡力，杆就不能平衡。所以对杆的作用力方向的分析，千万不能将其当做绳对待。对于轻杆平衡时，它只有两上端点所受的力，这两个力一定是一对平衡力。以 C点为研究对象，作出C点受力图如图所示。物体对C点向下的拉力大小等于重力mg，绳AC的拉力T沿绳指向A，硬杆对C点的弹力N，由于硬杆的质量不计，故杆的弹力N方向沿BC的连线方向，同时有几何关系
。图中的T和mg的合力与N是一对平衡力，且合力方向与T和mg的夹角均相同，由三角形知识可得T=mg 。
【答案】T=mg
11． 【解析】先分析B球受力情况，因OB处于竖直状态，拉力竖直向上，由平衡条件可知，B球只受重力和OB的拉力作用，线BA中无作用力。再分析A球受力，A球受重力、OA拉力和外力F，由平衡条件知该力可能是图F2、F3，选项B.C正确
【答案】B.C
12．【解析】将滑轮挂到细绳上，对滑轮进行受力分析如图所示，滑轮受到重力和AK和BK的拉力F，且两拉力相等，由于对称，因此重力作用线必过AK和BK的角平分线。延长AK交墙壁于C点，因KB =KC，所以由已知条件 AK+ KC = AC=2AO，所以图中的角度α =30°，此即两拉力与重力作用线的夹角。两个拉力的合力R与重力等值反向，所以：
2 F cos30° = R =G， 所以F = mg/2cos30° = 
mg/3 。
【答案】 mg/3
13．【解析】因光滑挂钩与轻滑轮模型相同，轻质挂钩的受力如图所示，
由平衡条件可知，T1、T2合力与G等大反向，且T1=T2。
所以 T1sinα
+T2sinα =T3= G
即T1=T2=
，而
AO?cosα+BO.cosα= CD，
所以 cosα =0.8
sin
=0.6，T1=T2=10N
【答案】10N
14．【解析】分析物体受力情况，选斜面方向为x 轴，垂直斜面方向为y 轴，把不在轴上的重力G
水平分力F分解到坐标轴上，由于物体处于平衡状态，则有
…
解得：
【答案】
15．【解析】如图所示，利用直尺、皮卷尺、漏斗、细沙等实验器材，用装满细沙漏斗朝水平地面堆积，从漏斗中落下的细沙总是在地面上形成一个小圆锥体，继续下落时，细沙由圆锥面表面下滑，当圆锥体的母线与地面的夹角达到一定角度时，细沙不再下滑，用直尺测量小圆锥体高度h，皮卷尺测量小圆锥体底面周长C，则由
得
。
【答案】
16．【解析】（1）当砂轮静止时，把AB杆和工件看成一个物体，它受到的外力对A轴的力矩有：重力的力矩（
）砂轮对工件的支持力的力矩
,
的力矩
由力矩的平衡，得
解得
代入数据得
（2）当砂轮转动时，除重力、支持力和
的力矩外，还有砂轮作用于工件的摩擦力的力矩
。由力矩的平平衡；得
解得
代入数据得
【答案】（1）
（2）
17．【解析】(1)空载时，杆杆秤恰好平衡，秤杆、配重物及挂钩所受重力相对提纽的合力矩Ｍ正好等于两套筒相对于提纽的力矩. 提纽到挂钩的距离为ｄ＝2cm，套筒的长Ｌ＝16cm. 此时，两套筒重心到提纽的距离为(Ｌ/2－ｄ). 两套筒质量ｍ＝0.1kg.
则Ｍ＝2ｍｇ(Ｌ/2－ｄ)＝0.12Nm.
(2)当在秤钩上挂一物体时，挂钩处增加一个重力ｍ1ｇ，它产生一个逆时针方向的力矩ｍ1ｇｄ应当与由于两套筒向右移动增加的力矩相平衡，则
ｍ1ｇｄ＝ｍｇＸ1＋ｍｇ(Ｘ1＋Ｘ2)，其中Ｘ1＝5cm、Ｘ2＝8cm为两套筒右移距离.
代入数据解得待测物体质量ｍ1＝0.9 kg.
(3)注意该杆秤的刻度特点：内层刻度是依据内层左侧与秤的最左端的距离来刻的、外层刻度是依据外层左侧与内层左侧的距离来刻的. 外层套筒丢失前，挂物ｍ2ｇ＝1kg，内层刻度为1kg，外层刻度为零，此时内、外层共同向右移动Ｘ杆秤力矩平衡. 则
ｍ2ｇｄ＝2ｍｇＸ，得Ｘ＝ｍ2ｄ/(2ｍ)＝0.1m.
由于外层套筒丢失，内层读数为1kg时，内筒左端离提纽的距离为Ｘ－ｄ，内筒重心离提纽的距离为(Ｘ－ｄ＋Ｌ/2)，此时内筒所产生的力矩与待测物产生力矩ｍ3ｇｄ及力矩Ｍ相平衡，即ｍ3ｇｄ＋Ｍ＝ｍｇ(Ｘ－ｄ＋Ｌ/2)，代入数据解得待测物质量ｍ3＝0.2kg.
【答案】（1）0.12Nm （2）0.9 kg. （3）ｍ3＝0.2kg.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com