如图所示，图形（1）、（2）、（3）（4）分别由两个相同的正三角形、正方形、正五边形、正六边形组成．本题中我们探索各图形顶点、边数、区域三者之间的关系．（例我们规定如图（2）的顶点数为16；边数为24，像，为边，不能再算边，边与边不能重叠；区域数为9，它们由八个小三角形区域和中间区域组成，它们相互独立．）

（1）每个图形中各有多少个顶点？多少条边？多少个区域？请将结果填入表格中．

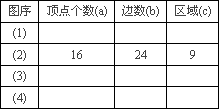
图序	顶点个数（）	边数（）	区域（）
（1）
（2）	16	24	9
（3）
（4）

（2）根据（1）中的结论，写出三者之间的关系表达式．

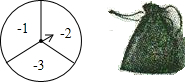如图所示，甲、乙两人玩游戏，他们准备了1个可以自由转动的转盘和一个不透明的袋子．转盘被分成面积相等的三个扇形，并在每一个扇形内分别标上数字-1，-2，-3；袋子中装有除数字以外其它均相同的三个乒乓球，球上标有数字1，2，3．游戏规则：转动转盘，当转盘停止后，指针所指区域的数字与随机从袋中摸出乒乓球的数字之和为0时，甲获胜；其它情况乙获胜．（如果指针恰好指在分界线上，那么重转一次，直到指针指向某一区域为止）
（1）用树状图或列表法求甲获胜的概率；
（2）这个游戏规则对甲乙双方公平吗？请判断并说明理由．

如图所示，在直角梯形ABCD中，∠D=∠C=90°，AB=4，BC=6，AD=8，点P、Q同时从A点出发，分别做匀速运动，其中点P沿AB、BC向终点C运动，速度为每秒2个单位，点Q沿AD向终点D运动，速度为每秒1个单位，当这两点中有一个点到达自己的终点时，另一个点也停止运动，设这两个点从出发运动了t秒．
（1）动点P与Q哪一点先到达自己的终点？此时t为何值；
（2）当O＜t＜2时，写出△PQA的面积S与时间t的函数关系式；
（3）以PQ为直径的圆能否与CD相切？若有可能，求出t的值或t的取值范围；若不可能，请说明理由．

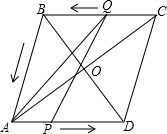如图所示，在菱形ABCD中，对角线AC、BD相交于点O，AC=8，BD=6．现有两动点P、Q分别从A、C两点同时出发，点P以每秒1个单位长的速度由点A向点D做匀速运动，点Q沿折线CB-BA向点A做匀速运动．
（1）菱形ABCD的边长为；
（2）若点Q的速度为每秒2个单位长，设运动时间为t秒．
①求△APQ的面积S关于t的函数关系式；
②当t为何值时，S有最大值，最大值是多少？
（3）若点Q的速度为每秒a个单位长（a≤

5

4

），当t=4秒时，△APQ是等腰三角形，请直接写出a的值．