
题目列表(包括答案和解析)
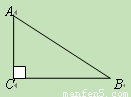
(11·珠海)(本题满分6分)如图,在Rt△ABC中,∠C=90°.
(1)求作:△ABC的一条中位线,与AB交于D点,与BC交于E点.(保留作图痕迹,不
写作法)
(2)若AC=6,AB=10,连结CD,则DE=_ ▲ ,CD=_ ▲ .


 经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.
经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.(本题满分7分)如图,斜坡AC的坡度(坡比)为1: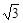 ,AC=10米.坡顶有
,AC=10米.坡顶有
一旗杆BC,旗杆顶端B点与A点有一条彩带AB相连,AB=14米.试求旗杆BC的高度.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com