
题目列表(包括答案和解析)
把一块三角尺放在边长为1的正方形ABCD上,并让它的直角顶点P在对角线AC上滑动,一条直角边始终经过点B,另一条直角边与射线DC相交于Q.设A,P两点间的距离为x,当点P在AC上滑动时,△PCQ是否可能成为等腰三角形?若可能,请指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;若不可能,请说明理由.
如图,抛物线 =-
=-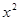 +5
+5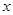 +
+ 经过点C(4,0),与
经过点C(4,0),与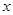 轴交于另一点A,与
轴交于另一点A,与 轴交于点B.
轴交于点B.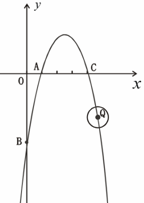
(1)求点A、B的坐标;
(2)P是 轴上一点,△PAB是等腰三角形,试求P点坐标;
轴上一点,△PAB是等腰三角形,试求P点坐标;
(3)若·Q的半径为1,圆心Q在抛物线上运动,当·Q与 轴相切时,求·Q上的点到点B的最短距离.
轴相切时,求·Q上的点到点B的最短距离.
如图,抛物线 =-
=-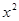 +5
+5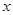 +
+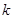 经过点C(4,0),与
经过点C(4,0),与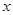 轴交于另一点A,与
轴交于另一点A,与 轴交于点B.
轴交于点B.

(1)求点A、B的坐标;
(2)P是 轴上一点,△PAB是等腰三角形,试求P点坐标;
轴上一点,△PAB是等腰三角形,试求P点坐标;
(3)若·Q的半径为1,圆心Q在抛物线上运动,当·Q与 轴相切时,求·Q上的点到点B的最短距离.
轴相切时,求·Q上的点到点B的最短距离.
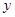 =-
=-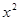 +5
+5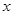 +
+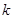 经过点C(4,0),与
经过点C(4,0),与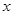 轴交于另一点A,与
轴交于另一点A,与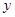 轴交于点B.
轴交于点B.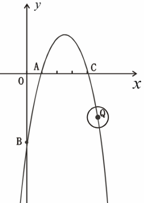
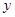 轴上一点,△PAB是等腰三角形,试求P点坐标;
轴上一点,△PAB是等腰三角形,试求P点坐标;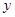 轴相切时,求·Q上的点到点B的最短距离.
轴相切时,求·Q上的点到点B的最短距离.如图,直线![]() 与x轴交于点A,与y轴交于点C。抛物线
与x轴交于点A,与y轴交于点C。抛物线![]() 经过点A、C,与x轴的另一个交点B
经过点A、C,与x轴的另一个交点B
(1)求抛物线解析式;
(2)点A到线段BC的距离;
(3)在x轴上是否存在点P使∠PCA = 45°,若存在请求出P点坐标,若不存在请说明理由;
(4)如图,N为抛物线对称轴一点且使△ANB为等腰直角三角形,Q为第一象限内对称轴左侧任意一点(不与A、N重合),且使∠AQB = 90°,下列两个结论:
①![]() 为定值;②
为定值;②![]() 为定值.其中只有一个结论正确,试证明正确的结论并求其值.
为定值.其中只有一个结论正确,试证明正确的结论并求其值.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com