
题目列表(包括答案和解析)
(本小题满分10分)
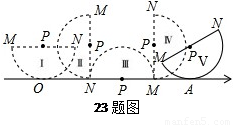
如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中半⊙P与数轴相切于点A,且此时△MPA为等边三角形.
 解答下列问题:(各小问结果保留π)
解答下列问题:(各小问结果保留π)
(1)位置Ⅰ中的点O到直线MN的距离为 ;
位置Ⅱ中的半⊙P与数轴的位置关系是 ;
(2)位置Ⅲ中的圆心P在数轴上表示的数为 ;
(3)求OA的长.
 解答下列问题:(各小问结果保留π)
解答下列问题:(各小问结果保留π)(本小题满分10分)
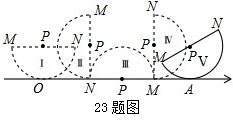
如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中半⊙P与数轴相切于点A,且此时△MPA为等边三角形.
 解答下列问题:(各小问结果保留π)
解答下列问题:(各小问结果保留π)
(1)位置Ⅰ中的点O到直线MN的距离为 ;
位置Ⅱ中的半⊙P与数轴的位置关系是 ;
(2)位置Ⅲ中的圆心P在数轴上表示的数为 ;
(3)求OA的长.
(本小题满分10分)
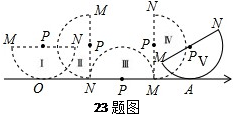
如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中半⊙P与数轴相切于点A,且此时△MPA为等边三角形. 解答下列问题:(各小问结果保留π)
解答下列问题:(各小问结果保留π)
(1)位置Ⅰ中的点O到直线MN的距离为 ;
位置Ⅱ中的半⊙P与数轴的位置关系是 ;
(2)位置Ⅲ中的圆心P在数轴上表示的数为 ;
(3)求OA的长.
(本小题满分8分)
已知:如图,在正方形ABCD中,点E、F分别在BC和CD上,AE = AF.
(1)求证:BE = DF;
(2)连接AC交EF于点O,延长OC至点M,使OM = OA,连接EM、FM.判断四边形AEMF是什么特殊四边形?并证明你的结论.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com