
题目列表(包括答案和解析)


 与x轴交A、B两点(A点在B点左侧),直线
与x轴交A、B两点(A点在B点左侧),直线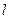 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.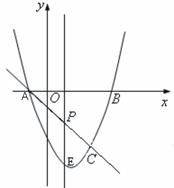
(本小题满分6分)设边长为2a的正方形的中心A在直线l上,它的一组对边垂直于直线l,半径为r的⊙O的圆心O在直线l上运动,点A、O间距离为d.
1.(1)如图①,当r<a时,根据d与a、r之间关系,请你将⊙O与正方形的公共点个数
填入下表:
2.(2)如图②,当r=a时,根据d与a、r之间关系,
请你写出⊙O与正方形的公共点个数。
当r=a时,⊙O与正方形的公共点个数可能有 个;
3.(3)如图③,当⊙O与正方形有5个公共点时,
r= (请用a的代数式表示r,不必说理)

(本小题满分9分)已知:如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.
 |
(本小题满分9分)
 如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的
如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的![]() ,另一根露出水面的长度是它的
,另一根露出水面的长度是它的![]() .两根铁棒长度之和为55 cm.
.两根铁棒长度之和为55 cm.
(1)根据题意,甲、乙两个同学分别列出了尚不完整的方程(组)如下:
![]() 甲:
甲: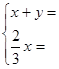 乙:
乙:![]() =55
=55
根据甲、乙两名同学所列的方程(组),请你分别指出未知数x,y表示的意义,然后在横线上补全甲、乙两名同学所列的方程(组):
甲:x表示 ,y表示 ;
乙:x表示 ;
(2)求此时木桶中水的深度多少cm?(写出完整的解答过程)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com