
题目列表(包括答案和解析)
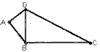
如图,梯形ABCD中,AD∥BC,∠BAD=90°,CE⊥AD于点E,AD=8cm,BC=4cm,AB=5cm。从初始时刻开始,动点P,Q 分别从点A,B同时出发,运动速度均为1 cm /s, 动点P沿A-B--C--E的方向运动,到点E停止;动点Q沿B--C--E--D的方向运动,到点D停止,设运动时间为![]() s,
s,![]() PA Q的面积为y cm2,(这里规定:线段是面积为0的三角形)
PA Q的面积为y cm2,(这里规定:线段是面积为0的三角形)
解答下列问题:
(1) 当x=2s时,y=_____ cm2;当![]() =
= ![]() s时,y=_______ cm2
s时,y=_______ cm2
(2)当5 ≤ x ≤ 14 时,求y与![]() 之间的函数关系式。
之间的函数关系式。
(3)当动点P在线段BC上运动时,求出![]() S梯形ABCD时
S梯形ABCD时![]() 的值。
的值。
(4)直接写出在整个运动过程中,使PQ与四边形ABCE的对角线平行的所有x的值.

| ||
| 3 |
| ||
| 3 |

| 1 |
| 2 |
| 1 |
| 2 |
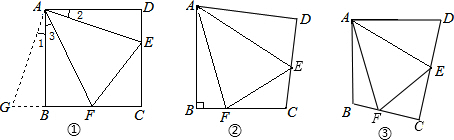
通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的。下面是一个案例,请补充完整。

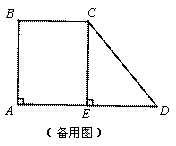
原题:如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,则EF=BE+DF,试说明理由。
(1)思路梳理
∵AB=CD,
∴把△ABE绕点A逆时针旋转90°至△ADG,可使AB与AD重合。
∵∠ADC=∠B=90°,
∴∠FDG=180°,点F、D、G共线。
根据 ,易证△AFG≌ ,得EF=BE+DF。
(2)类比引申
如图2,四边形ABCD中,AB=AD,∠BAD=90°,点E、F分别在边BC、CD上,∠EAF=45°。若∠B、∠D都不是直角,则当∠B与∠D满足等量关系 时,仍有EF=BE+DF。
(3)联想拓展
如图3,在△ABC中,∠BAC=90°,AB=AC,点D、E均在边BC上,且∠DAE=45°。猜想BD、DE、EC应满足的等量关系,并写出推理过程。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com